Drehimpulsquelle und Bahndrehimpuls

Ein System kann Impuls speichern und auf drei verschiedene Arten austauschen. Die Stärke des leitungsartigen Impulstransports bezüglich der Systemoberfläche und des quellenartigen Austausches mit dem Gravitationsfeld nennt man Kraft. Eine analoge Unterscheidung macht beim Drehimpuls wenig Sinn, weil der Drehimpuls nicht lokalisierbar ist. Eine Dichte oder eine Stromdichte wie bei der elektrischen Ladung, dem Impuls oder der Entropie lässt sich beim Drehimpuls nicht definieren.

Geht man aber von ganzen Bauteilen aus, darf sehr wohl ein Drehimpulsinhalt, ein Drehimpulsstrom oder eine Drehimpulsquelle definiert werden. Drehimpuls kann aber auch in der gegenseitigen Bewegung zweier Körper als Bahndrehimpuls gespeichert sein.

Lernziele

Drehimpulsströme

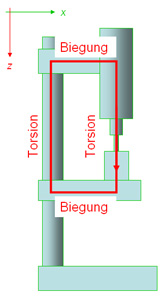
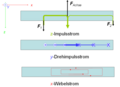
Drehimpulskreisstrom in einer Ständerbohrmaschine

Drehimpuls, der in einer Antriebswelle in seine eigene Richtung transportiert wird, verdreht die Welle zu einer Linksschraube. Wird ein Stab in Richtung einer Rechtsschraube verformt, fliesst der Drehimpuls gegen seine Bezugsrichtung. Drehimpulsströme werden wie elektrische Ströme oft im Kreis herum geführt, wie man am Beispiel der Ständerbohrmaschine gut erkennen kann. Sobald der Bohrer am Werkstück ansetzt, bildet sich ein Keisstrom aus. Dabei belädt der Motor den Drehimpulsstrom mit der Energie, die dieser bei der Schneide des Bohrers wieder frei setzt. Verfolgt man den ganzen Kreis, stellt man fest, dass der Drehimpulsstrom beim vorwärts und rückwärts Fliessen das Bauteil auf Torsion beansprucht. Im Bohrtisch und der Halterung des Motors erzeugt der seitwärts fliessende Drehimpuls dagegen Biegung. Legt man eine Schnitt- oder Referenzfläche quer zum Drehimpulsstrom, nennt man die beiden so definierten Drehmoment je nach Belastung Torsionsmoment oder Biegemoment.

Torsion

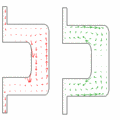
Drehimpulsströme lassen sich nur indirekt, über die sie begleitenden Impulsströme, nachweisen. Wird ein Bauteil auf Torsion belastet, muss der Drehimpulsstrom von einem Impulsstrom umhüllt sein. Zeigt die z-Achse in Richtung des Drehimpulstransportes, wird die in z-Richtung fliessende Drehimpulskomponente von einem z-Impulsstrom vollständig umhüllt. Stellt man sich die Stromlinien des Impulswirbels als Höhenlinie vor, entspricht das Volumen des zugehörigen Berges der Stärke des Drehimpulsstroms. Im geschlossenen Rohr zeichnen die Stromlinien des Impulswirbels einen voluminösen Tafelberg, während beim offenen U-Rohr nur eine atollförmige Struktur mit kleinem Volumen zu erkennen ist. Deshalb ist ein offenes U-Profil viel weniger torsionssteif als ein geschlossenes Rohr. Eine analoge "Verweichlichung" stellt sich ein, wenn man ein Kartonrohr längs einer Mantellinie aufschlitzt. Der im Karton fliessende Impulsstrom wird beim Schlitz zur Umkehr gezwungen. Durch das Aufschneiden des Rohres verwandelt sich der breite Tafelberg in ein schmales Atoll. Weil man die Dichte eines quer fliessenden Impulsstromes Schubspannung nennt, spricht der Ingenieur hier von der Schubflussumkehr beim Schlitz.

Vierkantrohr
U-Profil
geschlitztes Rohr

Biegung

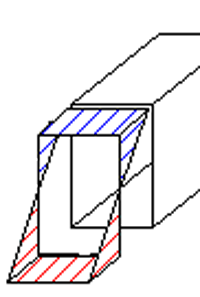
Drehimpuls, der quer zu seiner Bezugsrichtung fliesst, belastet das Bauteil auf Biegung. Im gebogenen Balken begrenzen seitlich verlaufende Impulsströme den Drehimpulstransport. Fliesst zum Beispiel z-Drehimpuls in x-Richtung, muss dieser Transport auf beiden Seiten, also in y-Richtung, durch einen x-Impulsstrom begrenzt sein. Ein H-Balken ist deshalb besonders biegesteif, weil in seinen Gurten grosse Impulsströme fliessen können. In einem Gurt fliesst der Impulsstrom vorwärts (Druck) und im andern rückwärts (Zug). So kann zwischen den beiden Gurten ein starker Drehimpulsstrom fliessen. Ein Vierkantprofil hat eine ähnliche Biegesteifigkeit wie der H-Träger, weist aber - wie weiter oben schon erklärt worden ist - zusätzlich noch eine grosse Torsionssteifigkeit auf.

Bei einem gebogenen Balken mit einem vollen Querschnitt nehmen die Zug- und Druckspannungen mit dem Abstand zur unbelasteten Mitte (neutralen Fasern) zu. Die Impulsströme sind demnach um so intensiver, je weiter entfernt sie von den neutralen Fasern durch den Balken fliessen. Analog zur Torsion darf man nun behaupten, dass der Drehimpulstrom in der Mitte des Querschnitts, bei den neutralen Fasern, am stärksten ist und nach aussen progressiv abnimmt: der Drehimpulsstrom nimmt in einem beliebigen Querschnitt an den Stellen am stärksten ab, an denen die grössten Impulsstromdichten auftreten. An den beiden Aussenflächen, dort wo die Impulsströme am intensivsten sind, geht die Stärke des Drehimpulsstroms auf Null zurück.

Spiegel

Betrachtet man die Bohrmaschine im Spiegel, fliesst der Drehimpuls in die andere Richtung, da im Spiegel eine Links- in eine Rechtsschraube übergeht. Weil gleichzeitig die Winkelgeschwindigkeit das Vorzeichen vertauscht, ändert sich am Energietransport nichts. Hinter dem Spiegel verwandelt sich ein rechtshändiges Koordinatensystem in ein linkshändiges, rechtsdrehende Propeller werden zu linksdrehenden und die Magnetfelder umhüllen den Strom im entgegen gesetzten Sinn. Dennoch ist die Welt hinter dem Spiegel für uns in Ordnung. Erst die neuere Physik hat gezeigt, dass es Prozesse gibt, die hinter dem Spiegel anders verlaufen als in der realen Welt.

Getriebe

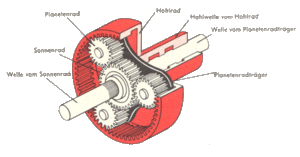
Bei jedem Getriebe treffen mindestens drei Drehimpulsströme aufeinander. Im Getriebe selber wird die Energie von einem Drehimpulsstrom auf einen andern umgeladen, wobei oft ein Drehimpulstrom ohne Energiebeladung über das Gehäuse fliesst. Anders beim Planetengetriebe! Bei diesem Gerät werden alle drei Drehimpulsströme über Wellen zu- oder abgeleitet. Da im stationären Betrieb aus der Drehimpulsbilanz ein Knotensatz wird, muss die Summe über alle drei Drehmomente gleich Null sein

[math]M_S+M_H+M_T=0[/math]

Arbeitet das Planetengetriebe reibungsfrei, ist die Summe über alle Energieströme (Leistungen der Drehmomente) ebenfalls gleich Null

[math]\omega_S M_S+\omega_H M_H+\omega_T M_T=0[/math]

Diese zwei Gleichungen verknüpfen zusammen mit der kinematischen Grundgleichung sechs Grössen (drei Winkelgeschwindigkeiten und drei Drehmomente).

Hebelgesetz

In einem verdrehten Balken fliesst der Drehimpuls in seine Bezugsrichtung, in einem gebogenen Balken seitwärts. Zudem wird jeder Drehimpulsstrom durch Impulsstöme begrenzt (ein umhüllender Wirbelstrom bei Torsion, zwei Berandungsströme bei Biegung). Diese bildhafte Vorstellung ist wohl korrekt, aber leider noch nicht umfassend. Wie beim Impuls treten beim Drehimpuls neben den eigentlichen Strömen auch noch Quellen auf. Diese Quellen werden durch das Hebelgesetz beschrieben.

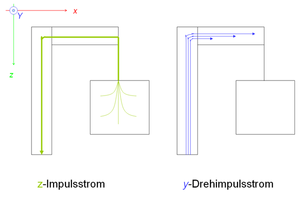
Betrachten wir dazu ein Körper, der an einem Galgen hängt. Der Galgen muss den vom Graviationsfeld zugeführten z-Impuls ableiten. Im Seil herrscht Zug, weil der Impuls gegen seine Bezugsrichtung abgeführt wird. Oben im Querbalken erzeugt dieser Impulsstrom eine Hebelwirkung. Der dort gegen die x-Achse fliessende z-Impulsstrom würde den ganzen Galgen in negativer Richtung um die y-Achse in Rotation versetzen, wenn dieser nicht im Boden verankert wäre. Wir erklären nun diese Wirkung mit Hilfe einer Drehimpulssenke (negative Quelle), deren Stärke proportional zur Stärke des querfliessenden Impulsstromes und zum zugehörigen Stromabschnitt ist

[math]\Sigma_{Ly}=\Delta x I_{pz}[/math]

Hier sind sowohl die Drehimpulssenke Σ_Ly als auch Δx negative Grössen. Die Drehimpulssenke wird nun vom Boden her gespiesen. Deshalb erfährt der vertikale Teil des Galgens eine konstante Biegung. Im horizontalen Teil nimmt die Biegung in Richtung der x-Achse ab. Im vertikalen Teil des Galgens fiesst der von der Last herkommende z-Impuls nach unten. Dieser primäre Impulsstrom wird durch einen viel stärkeren Kreisstrom überlagert, welcher den von unten nach oben fliessenden Drehimpulsstrom berandet.

Eine in positive x-Richtung fliessender z-Impulsstrom würde gemäss der oben formulierten Beziehung eine y-Drehimpulsquelle erzeugen. Nun induziert auch ein x-Impulsstrom, der in z-Richtung fliesst eine Senke bezüglich des y-Drehimpulses. Fasst man beide Einflüsse zusammen, erhält man

[math]\Sigma_{Ly}=\Delta x I_{pz}-\Delta z I_{px}[/math]

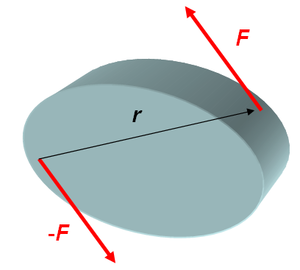
Indem man die Indices x, y und z zyklisch vertauscht, erhält man ein in Komponenten dargestelltes Vektorprodukt. Dieses Vektorprodukt beschreibt das Drehmoment eines Kräftepaares. Tritt nämlich ein beliebiger Impulsstrom in einen Körper ein und an einer andern Stelle wieder aus, bilden die Stromstärken an der Ein- und Austrittsfläche ein Kräftepaar (F, -F). Die durch den querfliessenden Impuls erzeugte Drehimpulsquelle darf nun als Drehmoment dem Kräftepaar zugeordnet werden

[math]\vec M=\vec r\times\vec F[/math]

Hier zeigt der Vektor r von der als negativ bezeichneten zur positiven Kraft des Paares.

Beispiel 1: Beim waagrechten, zweiarmigen Hebel mit angehängten Lasten, fliessen von beiden Seiten zwei z-Impulsströme gegen die Drehachse (erstes Bild unten). Dabei erzeugt der in positive x-Richtung fliessende Strom eine Quelle und der von der andern Seite her kommende Strom eine Senke bezüglich des y-Drehimpulses. Zum Ausgleich muss im Hebel y-Drehimpuls von den Quellen zu den Senken, also in x-Richtung, transportiert werden. Dieser Drehimpusstrom nimmt von der Einleitung des einen z-Impulsstromes her gegen die Drehachse linear zu, um dann bis zur Stelle, wo der andere z-Impulsstrom eingeleitet wird, wieder auf Null abzufallen. Das Hebelgesetz sorgt dafür, dass sich die Quellen und Senken die Waage halten. Die den Drehimpulsstrom begrenzenden x-Impulsströme belasten den Hebel auf Zug (Oberseite des Hebels] und auf Druck (Unterseite des Hebels), wobei diese Stromstärken bei der Drehachse am stärksten sind. Dort würde der Hebel bei Überlast auch brechen.

Beispiel 2: Man zerbricht einen Bleistift, indem man ihn mit beiden Händen umfasst, die Daumen abspreizt und damit den Bleistift gegen die restlichen Finger drückt (zweites Bild unten). Damit erzeugt man mit beiden Händen im Bleistift je eine querfliessenden Impulsstrom (grün), die eine Quelle bzw. eine Senke für bezüglich des Drehimpulses bilden (nicht skizziert). Der Drehimpuls der von den Quellen zu den Senken fliesst, erzeugt einen Impulswirbelstrom (rot), der den Stift schlussendlich zerstört.

Beispiel 3: Wirbelströme bilden sich auch dann, wenn das Hebelgesetz nicht direkt angewendet werden kann. Setzt man zum Beispiel einen Bügel unter Zug (drittes Bild unten), erzeugt der durchfliessende Impulsstrom (rot) beim seitwärts Fliessen Quellen und Senken bezüglich des Drehimpulses (nicht skizziert). Der dadurch erzwungene Drehimpulsstrom muss wiederum von Wirbelströmen umflossen sein (grün in den beiden Schenkeln und rot im mittleren Teil).

Zweiarmiger Hebel
Bleistift zerbrechen
Bügel unter Zug

Bahndrehimpuls

Eine um ihre Symmetrieachse rotierender Unterlegscheibe (Innenradius r, Aussenradius R, Dicke d, Dichte ρ) bildet eine stationäre Impulsverteilung. Der durch die Bewegung der Scheibe verursachte, konvektive Impulsstrom wird durch einen leitungsartigen Strom exakt kompensiert. Dieser gegen die Bewegung fliessende Impulsstrom setzt die Scheibe unter Zugspannung. Legt man eine Referenzfläche in radialer Richtung quer durch die Unterlegscheibe, muss die Stärke des konvektiven Impulsstromes bezüglich der Fläche [math]A=d(R-r)[/math] gleich der Stärke des leitungsartigen Impulsstromes (Zugkraft) sein

[math]I_{p_{conv}}=vI_m=v\varrho I_V=\varrho A v^2= A\sigma=I_{p_{leit}}=F[/math]

Für die Zugspannung σ (Dichte des leitungsartigen Impulsstromes) gilt deshalb

[math]\sigma=\varrho v^2[/math]

Die rotierende Unterlegscheibe, speichert Drehimpuls. Analog zu den stationärern Strömen darf man postulieren, dass der Drehimpuls in der Rotationsebene von Impuls "umhüllt" sein muss. Weil die wenigsten rotierenden Körper so schön symmetrisch wie die Unterlegscheibe sind, muss der Drehimpuls den einzelnen Teilen des rotierenden Körpers zugeordnet werden. Dies geschieht mit Hilfe des Bahndrehimpulses. Jedem Teilkörper eines rotierenden Systems darf ein Bahndrehimpuls bezüglich des Gesamtmassenmittelpunktes zugewiesen werden

[math]\vec L_B=\vec r\times\vec p[/math]

Wobei der Vektor r vom Massenmittelpunkt zum Teilkörper zeigt und der Impuls p des Teilkörpers auf ein System bezogen wird, in welchem der Massenmittelpunkt ruht.

Die Definition des Bahndrehimpulses ermöglicht die Berechnung eines Massenträgheitsmoments. Dazu zerlegen wir den mit der Winkelgeschwindigkeit ω rotierenden Körper in kleine Teil. Der Gesamtdrehimpuls ist dann gleich der Summe über alle Bahndrehimpulse der Einzelteile

[math]\vec L=\sum_i(\vec r_i\times\vec p_i)=\sum_i(\vec r_i\times\vec m_i v_i)=\sum_i\left(\vec r_i\times\vec m_i (\omega\times r_i)\right)[/math]

Die Winkelgeschwindigkeit kann ausgeklammert und das doppelte Vektorprodukt durch ein gewöhnliches ersetzt werden. Dazu führen wir den Radius R_i ein, der von der normal von der momentanen Drehachse weg um Teilkörper i zeigt

[math]L=\left(\sum_i m_i R_i^2\right)\omega=J\omega[/math]

Kontrollfragen

Zurück zum Inhalt