Entropie und Enthalpie

Heizen heisst Entropie zuführen und zum Kühlen muss man Entropie abführen. Trotzdem hat man Mitte des neunzehnten Jahrhunderts die beim Heizen und Kühlen mit transportierte Energie als Wärme definiert. Der Grund für diese aus heutiger Sicht verfehlte Definition liegt bei der Entropie selber. Um dies zu verdeutlichen, vergleichen wir zwei analoge Prozesse

Stossen zwei Autos frontal aufeinander, fliesst der Impuls von einem Auto ins andere, bis sich die Geschwindigkeiten angeglichen haben. In den Knautschzonen wird mit der vom Impuls freigesetzten Energie Entropie erzeugt.
Giesst man kaltes und warmes Wasser in einem isolierten Mischgefäss (Kalorimeter) zusammen, überträgt das heisse Wasser einen Teil seiner Entropie ans kalte. In der Mischzone wird mit der von der Entropie freigesetzten Energie zusätzlich Entropie erzeugt.

Der Impuls bleibt erhalten und die mechanisch verfügbare Energie nimmt ab, derweil die Entropie zunimmt und die thermisch verfügbare Energie erhalten bleibt. Die Formel Wärme gleich Energie hat sich gegen die viel tiefgründigere Identifikation Wärme gleich Entropie durchgesetzt, weil man früher gemeint hat, eine bilanzierfähige (mengenartige) Grösse müsse auch erhalten sein.

In dieser Vorlesung wollen wir uns mit der Energie und der Entropie homogener Speicher beschäftigen.

Lernziele

Bilanzgleichungen

Führt man einem System Wärme zu oder ab, kann bezüglich des Systems eine Entropiebilanz aufgestellt werden

[math]I_S=\dot S[/math]

Ist das System homogen, herrscht also an der Systemoberfläche die gleich Temperatur wie im Innern, darf die ganze Gleichung mit dieser (absoluten) Temperatur multipliziert werden. Links steht dann der zugeordnete Energiestrom, also nach offizieller Lesart der Wärmestrom, und rechts die Änderungsrate der inneren Energie

[math]I_{W_{therm}}=\dot W[/math]

Diese Energiebilanz ist korrekt, falls das Volumen des Systems konstant bleibt. Man spricht dann vom isochoren Heizen (griech. choros für Tanzplatz). Heizt man dagegen bei konstantem Druck, nennt man den Vorgang isobar. In der Regel tauscht ein Stoff beim isobaren Heizen auch noch mechanische Energie mit der Umgebung aus. Die Energiebilanz umfasst dann mindestens drei Terme, einen thermischen und einen mechanischen Energiestrom sowie die Änderungsrate der inneren Energie. In dieser allgemeineren Form heisst die Energiebilanz auch erster Hauptsatz der Thermodynamik.

Carnotor

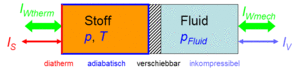
Wärmekraftmaschinen und Wärmepumpen arbeiten mit Stoffen die gasförmig oder zum Teil flüssig sind. Dabei spielen Expansion und Kompression sowie Heizen und Kühlen eine wesentliche Rolle. Um diese Prozesse kontrolliert ablaufen lassen, stellen wir uns ein Gerät, Carnotor genannt, vor. Dieses ideale Gerät besteht aus einem Doppelzylinder mit reibungsfrei verschiebbarem Kolben. Auf der einen Seite befindet sich der zu untersuchende, flüssige oder gasförmige Stoff. Die andere Seite ist mit einer inkompressiblen Hydraulikflüssigkeit gefüllt. Zylinderwand und Kolben sind adiabatisch (absolut wärmeundurchlässig), der Zylinderboden ist diatherm (ideal wärmedurchlässig). Nun kann man den Stoff heizen oder kühlen bzw. komprimieren oder dekomprimieren.

Vier Basisprozesse

Zum besseren Verständnis stellen wir uns vor, dass die Hydraulikflüssigkeit mit einer Pumpe und die Entropie mit einer Wärmepumpe hinein oder heraus gefördert wird. Vier Prozesse sind nun einfach zu realisieren

Name	Wärmepumpe	Hydraulikpumpe	Vorgang
isochor	in Betrieb	blockiert	Heizen oder Kühlen
isobar	in Betrieb	Freilauf	Heizen oder Kühlen
isentrop	blockiert	in Betrieb	Komprimieren oder Expandieren
isotherm	Freilauf	in Betrieb	Komprimieren oder Expandieren

Der Zustand "in Betrieb" bedeutet, dass die entsprechende Pumpe einen Strom erzeugt, also aktiv eine bestimmte Menge fördert. Im Zustand "blockiert" geht überhaupt kein Strom durch. Im "Freilauf" gleicht sich die Temperatur bzw. der Druck dem äusseren Potenzial an. In dieser Vorlesung beschäftigen wir uns nur mit dem isobaren Heizen bzw. Kühlen. Dabei wird Entropie zu- bzw. abgeführt und der Kolben hält einen bestimmten Druck aufrecht.

Änderungsraten

Bezüglich des (idealisierten Carnotors darf eine einfache Energiebilanz aufgestellt werden

[math]I_{W_{therm}}+I_{W_{hyd}}=TI_S+pI_V=\dot W[/math]

Weil zwischen Zufuhr und Speicherung mangels Temperaturgefälle keine Entropie erzeugt, gilt eine einfache Entropiebilanz

[math]I_S=\dot S[/math]

Die Volumenbilanz erstreckt sich auf zwei Kammern, wobei die Summe der beiden Änderungsrate immer gleich Null ist

[math]I_V=\dot V_{hyd}=-\dot V[/math]

Der Freilauf der Hydraulikpumpe und der reibungsfrei verschiebbare Kolben sorgen für eine homogene Druckverteilung. Weil zudem die Temperatur im ganzen Bilanzgebiet gleich gross ist, dürfen die Volumen- und die Entropiebilanz in die Energiebilanz eingesetzt werden

[math]T\dot S-p\dot V=\dot W[/math]

Diese Formel verknüpft die Änderung der inneren Energie mit den Änderungen der beiden mengenartigen Grössen Volumen und Entropie.

Wärme, innere Energie und Enthalpie

Wärme

Die Energie, die thermisch, also zusammen mit der Entropie über die Systemgrenze transportiert wird, heisst Wärme. Die Wärme hängt wie die Kraft mit einem Transport über die Systemoberfläche zusammen. Folglich gibt es in der Physik weder einen Wärmeinhalt noch eine Umwandlung von nutzbarer Energie in Wärme. Als Formelzeichen wird für die Wärme oft ein Q geschrieben und für den Wärmestrom [math]\dot Q[/math]. Weil wir in einer Bilanzgleichung den Punkt über einem Formelzeichen nur für die Änderungsrate verwenden und einer physikalischen Grösse möglichst immer mit das gleiche Formelzeichen zuweisen, schreiben wir für Wärme W_therm und für die Stärke eines Wärmestromes bezüglich einer Referenzfläche I_{W_therm}.

innere Energie

Die Energie, die in einem ruhenden System gespeichert ist, nennt man innere Energie. Das oft verwendete Formelzeichen für die innere Energie ist U. Wir schreiben weiterhin W für die Energie. Gemäss Albert Einstein ist die innere Energie gleich Masse mal das Quadrat der Lichtgeschwindigkeit. Weil die Einsteinsche Gleichsetzung von Masse und Energie einen unbrauchbar grossen Wert liefert, setzt man die innere Energie bei einem ausgewählten Zustand (Druck, Temperatur, Aggregatszustand) gleich Null. Im Gegensatz zur inneren Energie sind die Bewegungsenergie (kinetische Energie und Rotationsenergie) und die potentielle Energie äussere Energieformen. So hängen die kinetische Energie (zusammen mit dem Impuls gespeichert) und die Rotationsenegie (zusammen mit dem Drehimpuls gespeichert) vom Bewegungszustand des Beobachters (Bezugssystem) ab. Die potentielle Energie steckt im Gravitationsfeld bzw. im elektromagnetischen Feld und wird nur formal dem Körper zugerechnet.

Enthalpie

In unserer Umwelt hält die Luft den Druck konstant. Folglich laufen die meisten Heiz- oder Kühlvorgänge bei konstantem Druck, also isobar, ab. Untersucht man das isobare Heizen im Carnotor, stellt man fest, dass sich der Kolben durch die temperaturbedingte Ausdehnung bewegt und die Hydraulikflüssigkeit verdrängt. Die damit abgeführte Energie nennt man Expansionsarbeit. Weil man sich in diesem Fall nur für die Heizenergie interessiert, schreibt man die Energiebilanz um

[math]I_{W_{therm}}=\dot W-I_{W_{hyd}}=\dot W+p\dot V[/math]

Um diese Bilanz zu vereinfachen, definieren wir eine neue Energiegrösse, die Enthalpie H

[math]H=W+pV[/math]

Leitet man die Enthalpe bei konstantem Druck nach der Zeit ab, erhält man den rechten Term in der oben formulierten Energiebilanz

[math]I_{W_{therm}}=\dot H[/math]

Heizt man ein System bei konstantem Druck auf, ist die zugeführte Energie gleich der Änderung der Enthalpie

[math]W_{therm}=\Delta H[/math]

Diese Gleichung erklärt auch das Wort Enthalpie (griech. en „darin, innerhalb” und thalpos „Wärme“): beim isobaren Heizen entspricht die Enthalpieänderung der zugeführten Wärme; kühlt man bei gleichem Druck um die gleiche Temperaturdifferenz ab, ändert das System seine Enthalpie wieder um den gleichen Betrag und gibt diese Energiemenge in Form von Wärme ab, . Das Wort Enthalpie ist ein schönes Beispiel akademischer Unaufrichtigkeit. Weil man Wärme als thermisch ausgetauschte Energie definiert hat, aber trotzdem den Begriff Wärmeinhalt beibehalten möchte, nimmt man einfach das griechische Wort. Der Buchstabe H kommt übrigens vom englischen Wort heat content.

Die Enthalpie ist ein reiner Hilfsbegriff mit der Einheit Joule. Beim isobaren Heizen oder Kühlen fasst die Änderung der Enthalpie die Änderung der inneren Energie und die Expansions- bzw. Kompressionsarbeit in einem Ausdruck zusammen.

Eis, Wasser, Dampf

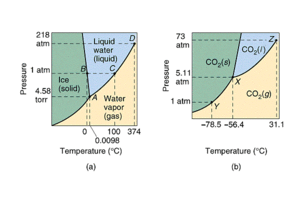
Führt man Eis von -20°C und Normaldruck (1013 mbar) kontinuierlich Wärme zu, steigt die Temperatur vorerst nur auf 0°C. Erst wenn alles Eis geschmolzen ist, erhöht sich die Temperatur weiter bis auf 100°C. Sobald alles Wasser verdampft ist, setzt ein erneuter Temperaturanstieg ein. Schmelz- und Verdampfungspunkt sind druckabhängig. Die Schmelztempertur T_s von Eis kann gesenkt werden, falls der Druck massiv zunimmt. Diesen Effekt nutzt man beim Schlittschuh laufen: unter den Kufen bildet sich infolge des dort herrschenden grossen Drucks ein dünner Wasserfilm, der die Reibung verkleinert. Die Verdampfungstemperatur T_v hängt stark vom Druck ab. Wird der Druck auf unter 30 mbar abgesenkt, verdampft Wasser schon bei Raumtemperatur. Im Reaktor eines Kernkraftwerkes hindert der hohe Druck von über 150 bar das 325°C heisse Wasser am Sieden. Im Phasendiagramm (p-T-Diagramm) können die Bereiche eingezeichnet werden, in denen die drei Aggregatszustände fest, flüssig und gasförmig stabil sind. Im Phasendiagramm sind die drei Zustandsgebiete durch die Sublimationsdruck-, die Schmelzdruck- und die Dampfdruckkurve getrennt. Bei CO₂ liegt der Schnittpunkt dieser drei Kurven, der Tripelpunkt, über dem Normaldruck. Deshalb sublimiert Trockeneis unter Zufuhr von Wärme.

Enthalpieänderung

Viele Festkörper, Flüssigkeiten und Gase erhöhen ihre Temperatur proportional zur zugeführten Wärme. Deshalb führt man eine Wärmekapapazität ein, die durch das Verhältnis von zugeführter Wärme und der damit verbundenen Temperaturerhöhung definiert ist

[math]C=\frac{Q}{\Delta T}=\frac{\Delta H}{\Delta T}[/math]

Die so definierte Wärmekapazität beschreibt die Enthalpieänderung pro Temperaturerhöhung bei konstant gehaltenem Druck. Eigentlich müsste man diese Grösse Enthalpiekapazität nennen, doch hat sich Wärmekapazität bei konstantem Druck eingebürgert.

Die Wärmekapazitäten für die verschiedenen Stoffe sind oft pro Kilogramm (spezifische Wärmekapazität c) tabelliert. In den gleichen Tabellenwerken findet man auch die spezifische Schmelzenthalpie q und die spezifische Verdampfungsenthalpie r, wobei speziell bei der Verdampfungsenthalpie auf den zugehörigen Druck geachtet werden muss. Je höher der Druck und damit die Verdampfungstemperatur, desto kleiner wird die Verdampfungsenthalpie.

Mit Hilfe der Stoffwerte spezifische Schmelenthalpie (q), Verdampfungsenthalpie (r) sowie den spezifischen Wärmekapazitäten c_fest, c_flüssig und c_gasförmig kann die isobare Enthalpieänderung vom Zustand {fest, Temperatur T₁} bis zum Zustand {gasförmig, Temperatur T₂} gerechnet werden

[math]\Delta H=m\left(c_{fe}(T_s-T_1)+q+c_{fl}(T_v-T_f)+r+c_p(T_2-T_v)\right)[/math]

Die Indizes für fest (fe) und flüssig (fl) werden oft weggelassen oder durch eine Abkürzung des entsprechenden Stoffs ersetzt. Bei Gasen schreibt man als Index ein p, um an den konstant zu haltenden Druck zu erinnern.

Beispiel 1: Ein thermisch isoliertes Mischgefäss, ein Kalorimeter, mit einer Wärmekapazität von 8 kJ/K enthält 1.2 Kilogramm Wasser und 800 Gramm Eis. Wie viel 80°C heisses Wasser muss ins Kalorimeter gegeben werden, damit sich die Temperatur auf 15°C erhöht?

Lösung: Bei isoliertem und isbarem Mischen bleibt die Enthalpie erhalten. Die Zunahme der Enthalpie (Schmelzen des Eises, Wasser und Kalorimeter auf 15°C erwärmen) muss gleich der Abnahme des sich von 80°C auf 15°C abkühlenden Wassers sein

[math]\Delta H_1+\Delta H_2=m_E q+(c(m_E+m_1)+C)(T_e-T_s)+m_2c(T_e-T_2)=0[/math]

demnach ist die gesuchte Masse gleich

[math]m_2=\frac{m_E q+(c(m_E+m_1)+C)(T_e-T_s)}{c(T_2-T_e)}[/math] = 1.88 kg

Entropieänderung

Die Änderungsrate der inneren Energie kann bei einem homogenen Stoff, wie oben mit dem Carnotor gezeigt, durch die Änderungsraten der Entropie und des Volumens ausgedrückt werden

[math]\dot W=T\dot S-p\dot V[/math]

Formt man diese Beziehung nach der Entropieänderungsrate um und hält den Druck konstant, ergibt sich

[math]\dot S=\frac{\dot W+p\dot V}{T}=\frac{\dot H}{T}[/math]

Beim isobaren Heizen ist die Änderungsrate der Entropie gleich der Änderungsrate der Enthalpie dividiert durch die Zeit. Diesen Zusammenhang lässt sich auch direkt über die Energie- und die Entropiebilanz sowie den zugeordneten Energiestrom herleiten

[math]\dot S=I_S=\frac{I_{W_{therm}}}{T}=\frac{\dot H}{T}[/math]

Aus dieser Beziehung folgt für die Schmelz- und die Verdampfungsentropie

[math]S_s=\frac{mq}{T_s}[/math] und [math]S_v=\frac{mr}{T_v}[/math]

Beim gewöhnlichen Aufheizen eines Stoffes unter konstantem Druck ist die Entropiezunahme gleich

[math]\Delta S=\int\dot S dt=\int\frac{\dot H}{T}dt=\int\frac{mc\dot T}{T}dt=\int_{T_1}^{T_2}\frac{mc}{T}dT=mc\ln{\frac{T_2}{T_1}}[/math]

Die letzte Umformung ist nur möglich, falls die spezifische Wärmekapazität c temperaturunabhängig ist.

Beispiel 2: 30 kg Wasser von 70° wird in 70 kg Wasser von 20°C gegossen. Welche Endtemperatur stellt sich ein? Wie viel Entropie wird dabei erzeugt? Der Einfluss des Mischgefässes ist zu vernachlässigen.

Lösung: Die Summe der beiden Enthalpieänderungen ist konstant

[math]\Delta H_1+\Delta H_2=m_1c(\vartheta-\vartheta_1)+m_2c(\vartheta-\vartheta_2)=0[/math]

Die Temperatur in Grad Celsius wird oft mit theta bezeichnet. Aus dieser Gleichsetzung folgt die einfach Mischformel, wonach die Endtemperatur gleich dem gewichteten Mittel der Einzeltemperaturen ist

[math]\vartheta=\frac{m_1\vartheta_1+m_2\vartheta_2}{m_1+m_2}[/math] = 35°C

Während des Mischvorgangs wird die folgende Entropiemenge produziert

[math]\Delta S=\Delta S_1+\Delta S_2=m_1c\ln{\frac{T}{T_1}}+m_2c\ln{\frac{T}{T_2}}[/math] = 1.12 kJ/K

Beispiel 3: 30 kg Wasser von 70° wird in 70 kg Wasser von 20°C werden mit Hilfe einer idealen Wärmekraftmaschine auf die gleiche Temperatur gebracht. Welche Endtemperatur stellt sich ein? Wie viel nutzbare Energie gibt die Wärmekraftmaschine ab? Der Einfluss des Mischgefässes ist zu vernachlässigen.

Lösung: Die ideale Wärmekraftmaschine sorgt dafür, dass die Entropie erhalten bleibt. Folglich gilt

[math]\Delta S_1+\Delta S_2=m_1c\ln{\frac{T}{T_1}}+m_2c\ln{\frac{T}{T_2}}=0[/math]

Daraus ergibt sich eine Mischtemperatur von

[math]T=T_1^{\frac{m_1}{m_1+m_2}}T_2^{\frac{m_2}{m_1+m_2}}[/math] = 307.2 K oder 34.2°C

Die von der Wärmekraftmaschine freigesetzte Energie ist dann gleich der Änderung der gesamten Enthalpie

[math]W=m_1c\Delta\vartheta_1+m_2c\Delta\vartheta_2[/math] = 344 kJ

Dies entspricht in etwa der im Beispiel 2 erzeugten Entropie mal die Mischtemperatur. Beim unkontrollierten Mischen von warmem und kaltem Wasser bleibt die Energie als Buchhaltungsgrösse erhalten. Dennoch geht nutzbare Energie "verloren". Diese Energie wird beim unkontrollierten Mischen an die zusätzlich produzierte Entropie gebunden.

molar statt spezifisch

Stoffwerte wie Wärmekapazität, Schmelz- oder Verdampfungsenthalpie sind in technischen Tabellenwerken meist spezifisch, also pro Kilogramm aufgelistet. In der Chemie bezieht man die Stoffeigenschaften meist auf ein Mol. Zur besseren Unterscheidung werden hier spezifische Grössen klein geschrieben und molare mit einem Hut versehen. Die Umrechnung von spezifisch in molar sollte man sich einmal an einem Beispiel überlegen. Wir machen das hier mit der Wärmekapazität C. Die gesamte Wärmekapazität eines Stoffes kann durch die spezifische oder durch die molare Kapazität ausgedrückt werden

[math]C=mc=n\hat c[/math]

Dividiert man die Masse durch die Stoffmenge, erhält man die Molmasse. Die molare Grösse ist demnach immer gleich der spezifischen Grösse multipliziert mit der Molmasse.

Kontrollfragen

Materialien

zurück zum Inhalt