Joule-Zyklus

Der Joule-Kreisprozess oder Brayton-Kreisprozess ist eine Idealisierung des in Gasturbinen und Strahltriebwerken ablaufenden Vorganges. Der Joule-Zyklus setzt sich aus zwei isentropen und zwei isobaren Zustandsänderungen zusammen.

Beschreibung

Im idealen Joule-Zyklus oder Joule-Kreisprozess wird das Gas isentrop kompimiert, isobar geheizt, isentrop entspannt und zum Schluss isobar gekühlt

1 - 2 isentrope Kompression (spezifische Entropie bleibt konstant)
2 - 3 isobares Heizen (Druck bleibt konstant)
3 - 4 isentrope Expansion (spezifische Entropie bleibt konstant)
4 - 1 isobares Kühlen (Druck bleibt konstant)

Zustandsdiagramme
T-s-Diagramm	p-v-Diagramm

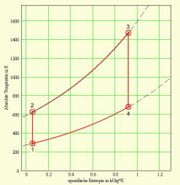
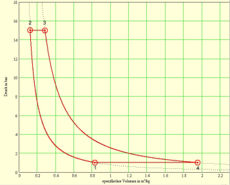
Die Fläche unter dem T-S-Diagramm entspricht der Wärme (thermisch ausgetauschte Energie) und die Fläche unter dem p-V-Diagramm der (negativen) Arbeit (mechanisch ausgetauschte Energie). Die ausgeschnittene Fläche ergibt in beiden Diagrammen die mechanisch frei gesetzte Energie. Die beiden Basisprozesse, aus denen der Joule-Zyklus zusammengesetzt wird, lassen sich thermisch, kalorisch oder entropisch beschreiben

Prozess	thermisch	entropisch	energetisch	Bemerkung
isobar	[math]\frac {v}{v_0}=\frac {T}{T_0}[/math]	[math]\Delta s=c_p ln\frac{T}{T_0}[/math]	[math]\Delta h=c_p\Delta T[/math]	Gesetz von Gay-Lussac
isentrop	[math](\frac{v}{v_0})^{R_s}=(\frac{T_0}{T})^{c_V}[/math]	[math]\Delta s=0[/math]	[math]\Delta w=c_V\Delta T[/math]	[math]\kappa=\frac{c_p}{c_V}[/math]

Die mengenartigen Grössen Entropie, Volumen, Energie und Enthalpie sind klein geschrieben, weil damit spezifische Grössen (Menge pro Masse) gemeint sind. Die Wärmekapazität bei konstantem Volumen c_V und bei konstantem Druck c_p sowie die Gaskonstante R_s sind ebenfalls auf die Masse bezogen (spezifisch). Die thermische Beschreibung für die isentrope Zustandsänderung kann mit Hilfe des Isentropenexponentes [math]\kappa = \frac {c_p}{c_V}[/math] umgeschrieben werden

[math](\frac{v}{v_0})^{\kappa -1}=\frac{T_0}{T}[/math]

Unter Verwendung der spezifischen Gasgleichung [math]pv=R_sT[/math] oder [math]p=\varrho R_sT[/math] lässt sich dieser Zusammenhang in eine Form mit den Variablen p und v umwandeln

[math](\frac{v}{v_0})^\kappa=\frac{p_0}{p}[/math]

Eine weitere Umformung liefert

[math](\frac{p}{p_0})^{\kappa -1}=(\frac{T}{T_0})^\kappa[/math]

maximale Leistung

Oft sind Druck und Temperatur im Punkt eins gegeben (z.B. bei Gasturbinen und Strahltriebwerke). Zudem darf die Gastemperatur beim Eintritt in die Turbine (T₃) einen bestimmten Wert Wert nicht überschreiten, weil sonst die Schaufeln beschädigt würden. Damit bleibt noch eine Grösse, die frei gewählt werden kann (z.B. der Druck nach dem Kompressor p₂). Komprimiert man nur wenig, darf lange geheizt werden, bis die maximale Turbineneintritts-Temperatur erreicht wird. Die vom Joule-Zyklus umrandete Fläche, die Nettoarbeit pro Kilogramm Luft, bildet dann im T-S-Diagramm eine schmale Sichel und im p-v-Diagramm ein flaches Rechteck mit zwei kurzen, gebogenen Kanten, den Isentropen. Wird die Luft komprimiert, bis sie beim Austritt aus dem Kompressor beinahe die Maximaltemperatur erreicht hat, darf sie nur noch wenig geheizt werden. Die umrandete Fläche bildet dann im T-S-Diagramm ein schmales Rechteck mit zwei gebogenen, kurzen Kanten, den Isobaren. Im p-v-Diagramm erscheint dieser Joule-Zyklus als feine Sichel. Zwischen den beiden Prozessführungen mit kleinem und grossem Druckverhältnis liegt ein Optimum, bei dem die Energie pro Kilogramm Gas maximal wird. Geht man von einem kontinuierlichen Gasstrom aus, ist dann die maximal mögliche Leistung unter den gegebenen Randbedingungen (minimaler Druck sowie tiefste und höchste Temperatur) erreicht.

Die nutzbare Energie pro Kilogramm Luft ist gleich der thermisch zugeführten Energie (spezifische Reaktionsenthalpie) minus der thermisch abgeführten Energie (Abwärme)

[math]w=c_p(T_3-T_2)+c_p(T_1-T_4)=c_p\left(T_3\left(1-\frac{T_4}{T_3}\right)+T_1\left(1-\frac{T_2}{T_1}\right)\right)[/math]

Zur Analyse führen wir folgende dimensionslose Kenngrössen ein

Druckverhältnis: [math]\pi=\frac{p_2}{p_1}=\frac{p_3}{p_4}[/math]

Temperaturverhältnis: [math]\tau=\frac{T_3}{T_1}[/math]

Mit der Abkürzung [math]\frac{\kappa-1}{\kappa}=m[/math] lassen sich bei den Isentropen die Temperaturverhältnisse in ein Druckverhältnis umschreiben

[math]\pi^m=\frac{T_2}{T_1}=\frac{T_3}{T_4}[/math]

Daraus folgt für die nutzbare Energie

[math]w=c_pT_1\left(\tau\left(1-\frac{1}{\pi^m}\right)+\left(1-\pi^m\right)\right)[/math]

Die nutzbare Energie ist gleich Null, falls das Druckverhältnis gleich 1 oder maximal ist [math]\left(\pi^m=\tau\right)[/math]. Um die maximale spezifische Energie zu bestimmen, leitet man die Energie nach dem Druckverhältnis ab und sucht die Nullstelle, was zu folgender Bedingung führt

[math]\tau=\pi^{2m}[/math] oder [math]\frac{T_3}{T_1}=\left(\frac{T_2}{T_1}\right)^2[/math]

Die Temperatur nach dem Kompressor entspricht damit dem geometrischen Mittel aus Turbinen- und Kompressor-Eingangstemperatur

[math]T_2=\sqrt{T_1T_3}[/math]

Die maximal nutzbare spezifische Energie ist somit gleich

[math]w=c_pT_1\left(\pi^{2m}-2\pi^m+1\right)=c_p\left(T_3-2\sqrt{T_1T_3}+T_1\right)=c_p\left(\sqrt{T_3}-\sqrt{T_1}\right)^2[/math]

Wirkungsgrad

Simulation

Der Joule-Zyklus kann mit Hilfe des Carnotor simuliert werden. Die nachfolgenden Bilder zeigen das Systemdiagramm des Carnotors, die Gleichungen sowie die beiden Zustandsdiagramme, das Temperatur-Entropie-Diagramm und das Druck-Volumen-Diagramm.