Pendel

Physisches Pendel

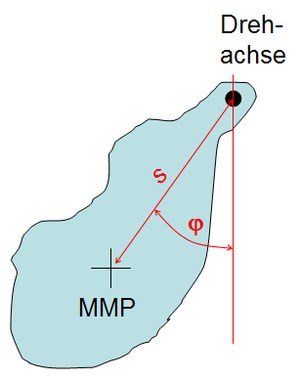
Ein Pendel (lat: pendere = hängen) besteht aus einem starren Körper, der um eine horizontal ausgerichtete Achse frei drehen kann. Lenkt man ein Pendel aus seiner Ruhelage aus und lässt es los, schwingt es unter dem Einfluss der Schwerkraft zurück. Danach pendelt es um die Gleichgewichtslage hin und her, bis es infolge der Reibung wieder zum Stillstand kommt.

Das Pendel kann als Rotator modelliert werden. In dieser hybriden Formulierung der Mechanik des starren Körpers bezieht man das die Kräfte begleitende Drehmoment auf die fixe Achse und fasst den Eigen- und Bahndrehimpuls in einem einzigen Speicher zusammen. Die unkontrolliert über die Achse fliessenden Impulsströme, die Zwangs- oder Führungskräfte, müssen so nicht berücksichtigt werden. Oft heisst das Modell eines realen Pendels auch physisches (körperliches) Pendel im Gegensatz zum mathematischen Pendel, bei dem ein Massenpunkt an einem masselosen Faden hin und her schwingt.

Theorie

Drehimpulsbilanz

Auf den Pendelkörper wirken zwei Kräfte, die Lagerkraft und die Gewichtskraft, ein. Mit der Gewichtskraft beschreibt man die Wirkung des Gravitationsfeldes bezüglich Translation und Rotation. Dazu ordnet man der gravitativen Impulsquelle einen Kraftpfeil zu, der im Massenmittelpunkt "angreift" und dessen Stärke gleich Masse m mal Gravitationsfeldstärke g ist. Weil in der Rotatormechanik die begleitenden Drehmomente auf die fixe Drehachse zu beziehen sind, muss nur der Gewichtskraft nicht aber der Lagerkraft ein Drehmoment zugeschrieben werden. Das die Gewichtskraft bezüglich der Drehachse begleitende Drehmoment ist dann gleich Gewichtskraft mal Horizontaldistanz zwischen Massenmittelpunkt und Drehachse (Abstand der Drehachse von der Wirklinie der Gewichtskraft).

Führt man nun einen Drehwinkel ein, der in der Gleichgewichtslage gleich Null ist, gilt für das der Gewichtskraft zugeordnete Drehmoment

[math]M_G = -mgs \sin \varphi[/math]

wobei s den Abstand des Massenmittelpunktes von der Drehachse beschreibt. Das Minuszeichen besagt, dass das von der "Gewichtskraft ausgeübte Drehmoment" immer rücktreibend wirkt.

Die Drehimpulsbilanz besagt nun, dass die vom Gravitationsfeld im Zusammenspiel mit der Achse erzeugte Drehmoment gleich der Änderungsrate des Drehimpulses ist

[math]{-}mgs \sin \varphi = \dot L[/math]

Ersetzt man den Drehimpulsinhalt durch das kapazitive Gesetz der Drehmechanik

[math]L = L_{eigen} + L_{Bahn} = J \dot \varphi + ms^2\dot \varphi = (J + ms^2)\dot \varphi [/math]

erhält man eine Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten

[math]{-}mgs \sin \varphi = \dot L =(J + ms^2)\ddot \varphi [/math]

Diese Differentialgleichung ist elementar nicht lösbar und erfordert Kenntnisse über elliptische Integrale. Deshalb wird sie üblicherweise linearisiert, indem man den Sinus des Auslenkwinkels gleich dem Winkel selber setzt.

[math]mgs \varphi +(J + ms^2)\ddot \varphi = 0[/math]

Lösung der Schwingungsgleichung

Mit der Linearisierung der Wirkung der Gewichtskraft erhält man die Differentialgleichung des harmonischen Oszillators

[math]mgs\varphi + (J + ms^2)\ddot \varphi = 0[/math]

Zur allgemeinen Lösung sei eine sinusförmige Änderung des Winkels φ mit der Zeit vorgschlagen

[math]\varphi = \varphi_0 \sin (\Omega t + \phi_0)[/math]

φ ist die Amplitude und Ω heisst Kreisfrequenz. Setzt man diesen Lösungsansatz in die Gleichung ein, ergibt sich die folgende Beziehung

[math]\varphi \left[mgs + (J + ms^2)\Omega^2 \right] = 0[/math]

Der Ansatz ist erfüllt, falls der Wert in der eckigen Klammer verschwindet. Dies führt zu folgender Forderung bezüglich der Kreisfrequenz

[math]\Omega = \sqrt{\frac {mgs}{J + ms^2}}[/math]

Weil das Produkt aus Kreisfrequenz und Schwingungsdauert T gleich 2π sein muss, berechnet sich die Schwindungsdauer wie folgt

[math]T = \frac {2\pi}{\Omega} = 2\pi \sqrt{\frac {J + ms^2}{mgs}}[/math]

Setzt man das Massenträgheitsmoment J gleich Null, kann das Pendel nur Bahndrehimpuls bezüglich der Drehachse und keinen Eigendrehimpuls speichern. Man spricht dann von einem mathematischen Pendel.

minimale Schwingungsdauer

Lässt man den Schwerpunkt des Pendels gegen die Drehachse wandern (s = 0), geht die Schwingungsdauer gegen unendlich. Liegt der Schwerpunkt weit von der Drehachse weg (s sehr gross), nimmt die Schwingungsdauer wieder mit s zu. Also muss es einen Abstand geben, bei dem die Schwingungsdauer minimal wird. Um diesen Abstand zu findet, leitet man die Formel für die Schwingungsdauer nach s ab und setzt den Wert gleich Null. Daraus folgt, dass die Schwinungsdauer minimal wird, wenn s gleich der Wurzel aus dem Quotienten von Massenträgheitsmoment und Masse ist

[math]s = \sqrt{\frac {J}{m}}[/math]

Modell

Systemdiagramm und Gleichungen des Pendels

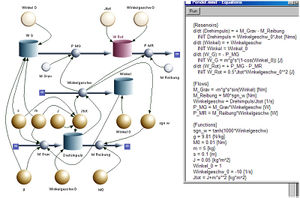
Das eigentliche Modell des Pendels umfasst die Drehimpulsbilanz und einen Integrator, der aus der Winkelgeschwindigkeit den Winkel berechnet. In der Drehimpulsbilanz wird das von der Gravitation verursachte Drehmoment sowie eine Lagerreibung berücksichtigt. Diese beiden Drehmomente erzeugen die Änderungsrate des Drehimpulses

[math]M_G + M_R = \dot L[/math]

Das gravitative Drehmoment gehorcht dem Hebelgesetz

[math]M_G = -mgs\sin(\varphi)[/math]

Die Lagerreibung hängt nur von der Richtung der Winkelgeschwindigkeit ab

[math]M_R = -M_{R0} sgn(\omega) = -M_{R0} \tanh(k \omega)[/math]

Der Tangenshyperbolicus erzeugt eine Funktion, deren Werte im negativen Bereich des Arguments grösser als -1 und im positiven Bereich kleiner als +1 ist. Der Faktor k, der viel grösser als 1 sein soll, sorgt dafür, dass die beiden Grenzwerte +1 und -1 möglichst schnell angenommen werden.

Die Winkelgeschwindigkeit ergibt sich aus dem Drehimpuls durch Division mit dem totalen Massenträgheitsmoment

[math]\dot \varphi = \frac {L}{J + ms^2}[/math]

Die Energiebilanz kann als zweite Beschreibungsebene ins Modell eingebaut werden. Die Leistung des von der Gravitation verursachten Drehmoments entspricht der Stärke des zwischen Gravitations- und Rotationsenergie hin und her fliessenden Energiestromes

[math]P(M_G) = M_G \omega = -mgs\sin(\varphi) \omega = -\dot W_G[/math]

Die Leistung des Reibdrehmoments beschreibt den Energiestrom, der vom Körper an die Umwelt abfliesst

[math]P(M_R) = M \omega = -M_{R0} sgn(\omega) \omega[/math]

Achtet man bei der Modellierung darauf, dass die Energieströme gleich gerichtet sind wie die Drehimpulsströme, berechnet sich jeder Energiestrom bezüglich eines Speichers als Drehimpulsstrom mal Winkelgeschwindigkeit des Speichers. Die Rotationsenergie ergibt sich so direkt aus der mit der Winkelgeschwindigkeit multiplizierten Drehimpulsbilanz

[math]M_G \omega + M_R \omega = \dot W_{rot}[/math]

Damit die Gravitationsenergie am tiefsten Punkt des Pendels gleich Null ist, setzt man als Startwert

[math]W_{G0} = m g s (1 - cos(\varphi))[/math]

Der Anfangswert der Rotationsenergie hängt vom Startwert des Drehimpulses ab

[math]W_{rot0} =L_0 \frac {\omega}{2} = \frac{1}{2} J \omega^2 = \frac{L_0^2}{2J}[/math]

Links

• Pendel auf Youtube