Tut 1.4

Ein Reservoir, das gefüllt und geleert wird, oder ein Körper, der von aufgeprägten Kräften beschleunigt wird, bilden noch keine dynamische Systeme. Erst wenn die gespeicherte Menge selber direkt oder indirekt auf die Zu- und Abflüsse zurück wirkt, kann von einem dynamischen System gesprochen werden. Mathematisch betrachtet bilden Flussgrössen, Bestandesgrössen und Rückkopplung (feed back) eine Differentialgleichung erster Ordnung.

Rückkopplungen

Reservoir mit Abfluss

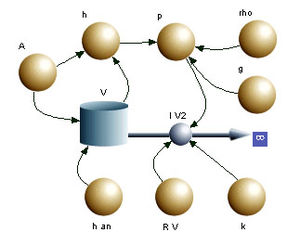
Eine System kann über eine oder mehrere Bestandesgrösse rückkoppeln. Die Zahl der beteiligten Bestandesgrössen legt die Ordnung der Differentialgleichung fest. Wir beschränken uns hier auf Systeme mit nur einer Bestandesgrösse. Die entsprechende Menge wird dann mit einer Umgebung ausgetauscht, die häufig einen fixen Bezugspunkt für das Potenzial oder die intensive Grösse aufweist. Das abgebildete Systemdiagramm eines Reservoirs zeigt nur einen Abfluss und keinen Zufluss. Die nachfolgende Liste enthält Beispiele mit einem von aussen gesteuerten (aufgeprägten) Zustrom und einem vom Zustand des Systems abhängigen Abfluss.

System	Menge	intensive Grösse	Abfluss
Reservoir	Volumen	Füllhöhe oder Druck	laminar oder turbulent
Mensch	Alkohol	Konzentration (Gewichtspromille)	über 0.2% konstant, danach linear
fallender Körper	Impuls	Geschwindigkeit	Luftwiderstand, quadratisch

negative und positive Rückkopplung

positives und negatives Feedback

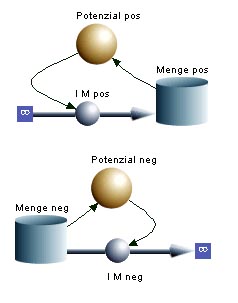
Wirkt die gespeicherte Menge über die intensive Grösse antreibend auf den Abfluss, spricht man von einer negativen Rückkopplung. Der Inhalt behindert dann das eigene Wachstum. Alle oben aufgeführten Beispiel sind negativ rückgekoppelt.

Fördert die gespeicherte Menge den Zufluss, spricht man von einer positiven Rückkopplung. Der Inhalt steigert dann das eigene Wachstum. Unbeschränkt rückgekoppelte Systeme zerstören sich in der Regel selber. Bei positiv rückgekoppelten Teilsysteme wird oft zuerst das Gesamtsystem kannibalisieren (Steuerwettbewerb).

Zurück zu Inhalt

Beispiel

Das oben abgebildete Systemdiagramm zeigt ein Reservoir, aus dem über ein langes dünnes Rohr Wasser abfliesst. Einzelne Parameter sind schon unter Parameter erklärt worden. Bei hohem Füllstand ist der Abfluss turbulent. Die Stärke des Abflusses nimmt dann mit der Wurzel aus dem Überdruck zu

[math]I_{V_2} = \sqrt{\frac {p}{k}}[/math]

Sinkt der Wasserspiegel unter die kritische Grenze, fliesst das Wasser laminar durch das Rohr weg. Bei laminarem Abfluss ist die Stromstärke proportional zum Überdruck p beim Gefässboden

[math]I_{V_2} = \frac {p}{R_V}[/math]

Füllhöhe und Abfluss in 1000 s

Die Konstante k und der Strömungswiderstand R_V sind so zu wählen, dass bei einem Füllstand von einem Meter, also bei einem Druck von 10 kPa, der Abfluss 0.01 m³/s beträgt und gerade von turbulent auf laminar umschlägt. Aus dieser Bedingung können die beiden Systemparameter berechnet werden

[math]k = \left(\frac {p}{(I_{V_2})^2}\right)_{krit}[/math] = 10⁸ Pa s²/m⁶

[math]R_V = \left(\frac {p}{I_{V_2}}\right)_{krit}[/math] = 10⁶ Pa s/m³

Damit der Umschlag beim kritischen Druck von 10 kPa auch wirklich passiert, schreibt man diese Bedingung in den Abfluss hinein:

I_V2 = if p > 1e4 then sqrt(p/k) else p/R_V

In hier gezeigten Modell ist der Zufluss aus dem Beispiel unter Parameter durch aktivieren des zugehörigen Objekts und Eingabe der Tastenkombination Ctrl + Delete entfernt worden.

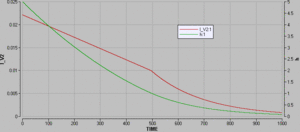
Die Graphik zeigt den Füllstand sowie die Stromstärke des Abflusses in Funktion der Zeit. Bei turbulentem Abfluss nimmt die Stromstärke linear und die Füllhöhe quadratisch in der Zeit ab. Der laminare Abfluss bildet zusammen mit dem Reservoir ein lineares RC-Glied. Bei linearen RC-Gliedern nimmt sowohl das Potenzial als auch die Stromstärke exponentiell mit der Zeit ab

[math]h = h_{an}e^{-t/\tau}[/math] mit [math]\tau = RC[/math]

Zurück zu Inhalt