Aviatik 2008/Ass: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: '''Erlaubte Hilfsmittel:''' Taschenrechner, selbstverfasste Formelsammlung '''Daten:''' {| |width="350"|Gravitationsfeldstärke |width="100"|9.81 N/kg |- |universell...) |
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
'''Daten:''' |
'''Daten:''' |
||
{| |
{| |
||
|width="350"|Gravitationsfeldstärke |
|width="350"|Gravitationsfeldstärke ''g'' |
||
|width="100"|9.81 N/kg |
|width="100"|9.81 N/kg |
||
|- |
|- |
||
| Zeile 10: | Zeile 10: | ||
|- |
|- |
||
|Dichte von Wasser |
|Dichte von Wasser |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
|1000 kg/m<sup>3</sup> |
|1000 kg/m<sup>3</sup> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
|- |
|- |
||
|Anzahl Freiheitsgrade der Luftmolekülen |
|Anzahl Freiheitsgrade der Luftmolekülen |
||
| Zeile 23: | Zeile 23: | ||
==Aufgabe 1== |
==Aufgabe 1== |
||
Ein [[Kondensator]] (Kapazität 4 mF oder 0.004 F), der auf eine Spannung von 5 V aufgeladen wurde, wird danach über einem Widerstandselement (Widerstand 150 Ω) entladen. |
|||
Mode |
|||
#Wie gross ist die Spannung über dem Kondensator eine Sekunde nach Schliessen des Schalters? |
|||
#Skizzieren Sie das [[Systemdiagramm]] (Flowchart) für dieses System. Schreiben Sie alle zur Modellierung notwendigen Gleichungen auf. |
|||
#Ergänzen Sie das Systemdiagramm so, dass die im Widerstand [[Dissipation|dissipierte]] Energie laufend berechnet wird. |
|||
#Nun wird der Widerstand durch eine ideale Spule (Induktivität 2 mH) ersetzt. Zeichnen Sie ein neues Systemdiagramm (ohne Energieberechnung) und schreiben Sie die notwendigen Gleichungen wiederum separat dazu. |
|||
==Aufgabe 2== |
==Aufgabe 2== |
||
Ein Güterwagen A (Masse unbekannt) prallt ungebremst mit einer Geschwindigkeit von 3 m/s in einen zweiten Wagen B (Masse 40 t), der anfänglich ruht und dessen Räder gebremst sind. In den beiden Diagrammen finden Sie die Geschwindigkeit des Wagens B sowie die totale [[Impulsstrom]]stärke zwischen den Wagen (totale Pufferkraft) in Funktion der Zeit. |
|||
Mode |
|||
#Wie gross ist die Reibungskraft auf den Wagen B zum Zeitpunkt 0.8 s? |
|||
#Wie weit verschiebt sich der Wagen B, bis er wieder still steht? |
|||
#Wie viel [[Impuls]] fliesst durch die Puffer bis die Wagen gleich schnell sind? Wie gross ist die Masse des Wagens A? |
|||
#Wie viel [[Energie]] wird in den ersten 0.3 Sekunden infolge Reibung zwischen Schiene und Räder des Wagens B dissipiert? |
|||
<gallery> |
|||
Bild:Aviatik 08 Ass 21.png|''v-t-''Diagramm |
|||
Bild:Aviatik 08 Ass 22.png|''F-t-''Diagramm |
|||
</gallery> |
|||
==Aufgabe 3== |
==Aufgabe 3== |
||
Im Schleudergang dreht sich die Trommel einer Waschmaschine (Durchmesser 40 cm) mit 1400 U/min (1400 RPM). Infolge einer Unachtsamkeit ist ein Fünffrankenstück (Masse 13,2 g) in die Maschine geraten und liegt nun direkt auf der Oberfläche der Trommel. Die Fragen beziehen sich auf einen [[Bezugssystem|Beobachter]], der in der Waschküche steht. |
|||
Mode |
|||
#Zeichnen Sie alle [[Kraft|Kräfte]] ein, die am höchsten Punkt der [[Kreisbewegung|Kreisbahn]] auf das Geldstück einwirken. Geben Sie diesen Kräften einen passenden Namen. |
|||
#Berechnen Sie die Beschleunigung des Geldstücks beim höchsten Punkt der Bahn. In welche Richtung zeigt der Beschleunigungsvektor? |
|||
#Wie gross ist die Kraft der Trommel auf das Geldstück am höchsten und am tiefsten Punkt der Bahn? Geben Sie die Kraft als Vielfaches der Gewichtskraft an. |
|||
==Aufgabe 4== |
==Aufgabe 4== |
||
Ein [[Turbofan]] (Eintrittsdurchmesser 1.6 m) erzeugt bei einer Luftdichte von 400 g/m<sup>3</sup> und einer Geschwindigkeit des Flugzeugs von 250 m/s eine Schubkraft von 50 kN. |
|||
Mode |
|||
#Berechnen Sie die Stärke des durch das Triebwerk fliessenden Massenstroms und ermitteln Sie dann die [[Geschwindigkeit]], mit der die Luft aus dem Triebwerk ausströmt. Idealisieren Sie dazu den Prozess, d.h. vernachlässigen Sie den Einfluss der Brennstoffzufuhr und nehmen Sie an, dass Kern- und Mantelstrom gleich schnell sind. |
|||
#Welche minimale Leistung würde dann (, wenn Kern- und Mantelstrom gleich schnell wären) das Triebwerk an den Luftstrom abgeben? |
|||
#Der Mantelstrom mache nun 80% des Luftstromes aus und trete halb so schnell wie der Kernstrom aus. Wie schnell tritt der Mantelstrom aus dem Triebwerk aus? |
|||
#Wie gross ist nun die minimale Leistung des Triebwerks? |
|||
==Aufgabe 5== |
==Aufgabe 5== |
||
600 kg Wasser sollen von 15°C auf 75°C erwärmt werden. Dazu vergleichen wir drei verschiedene Möglichkeiten miteinander: Widerstandsheizung, Wärmepumpe mit festen Ein- und Ausgangstemperaturen, absolut reversibles Heizen. |
|||
Mode |
|||
#Wie gross ist der Energiebedarf, wenn diese Wassermenge mit einer elektrischen Widerstandsheizung aufgewärmt werden muss. |
|||
#Wie gross ist der Energiebedarf, wenn das Wasser mit Hilfe einer [[Wärmepumpe]] aufgeheizt wird? Die Wärme wird durch die Wärmepumpe reversibel von 0°C auf 90°C gefördert und fliesst von dort irreversibel ins aufzuheizende Wasser. |
|||
#Wie viel [[Entropie]] wird in diesem Fall zwischen der Wärmepumpe und dem aufzuheizenden Wasser erzeugt? |
|||
#Wie gross ist der Energiebedarf, wenn die Entropie der 27°C warmen Umgebung entnommenen und verlustfrei dem aufzuheizenden Wasser zugeführt wird? |
|||
==Aufgabe 6== |
==Aufgabe 6== |
||
Der [[Stirling-Kreisprozess]] ist eine Idealisierung der in einem Stirling-Motor ablaufenden Vorgänge. Beim Stirling-Kreisprozess übernimmt ein Arbeitsgas Wärme bei konstanter Temperatur. Danach wird das Arbeitsgas isochor gekühlt, um dann im dritten Schritt Wärme isotherm abzugeben. Im vierten und letzten Teilprozess wird das Arbeitsgas isochor auf die ursprüngliche Temperatur erwärmt. |
|||
Mode |
|||
#Zeichnen Sie den Stirling-Kreisprozess im p-V-Diagramm und im T-S-Diagramm. |
|||
#Wie viel thermische Energie und wie viel [[Entropie]] nimmt ein Mol Helium bei 750 K auf, wenn sich das zugehörige Volumen von 1 Liter auf 3 Liter verdreifacht? |
|||
#Um welchen Wert ändert sich die [[innere Energie]] des Heliums, wenn es bei konstantem Volumen auf 300 K gekühlt wird? |
|||
#Weil das Arbeitsgas beim [[isochor]]en Abkühlen die Wärme an einen Zwischenspeicher abgibt und beim isochoren Aufheizen wieder von diesem bezieht, muss nur die zur [[isotherm]]en Expansion benötigte Wärme extern zugeführt werden. Berechnen Sie nun den [[Wirkungsgrad]] des Stirling-Kreisprozesses, d.h. das Verhältnis zwischen nutzbarer Nettoarbeit und extern zugeführter Energie. Für den Kreisprozess nehmen Sie die bei b) und c) genannten Werte für Gas, Temperatur und Volumen. |
|||
==Aufgabe 7== |
==Aufgabe 7== |
||
[[Bild:Aviatik 08 Ass 7.png|thumb|Fadenspule]]Auf eine ruhende Fadenspule (Masse 6 kg, [[Massenträgheitsmoment]] 0.1 kgm<sup>2</sup>, Abrollradius 30 cm, Wickelradius 20 cm) wirkt über einen horizontal ausgerichteten Faden eine [[Kraft]] ein. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N. |
|||
Mode |
|||
#[[Freischneiden|Schneiden]] Sie die Fadenspule frei, d.h. zeichnen Sie alle Kräfte ein, die auf die Spule wirken und formulieren Sie die drei [[Bilanz]]gleichungen, die Grundgesetze der Mechanik. |
|||
#Mit welcher maximalen [[Kraft]] kann am Faden gezogen werden, damit die Spule gerade nicht rutscht? |
|||
#Wie gross ist dann die Beschleunigung der Spulenachse? |
|||
#In einem zweiten Versuch zieht man mit 20 N. Die Reibkraft beträgt immer noch 10 N. Wie gross ist nun die Beschleunigung der Spulenachse? Welchen Wert nimmt die Winkelbeschleunigung an? |
|||
==Aufgabe 8== |
==Aufgabe 8== |
||
Ein Flugzeug fliegt mit einer Geschwindigkeit von 200 m/s durch eine horizontale Kurve (Radius 900 m). Der rotierende Teil des Turbojet-Strahltriebwerkes (Drehzahl 9000 U/min) hat eine Masse von 80 kg und weist ein [[Massenträgheitsmoment]] von 12 kgm<sup>2</sup> auf. |
|||
Mode |
|||
#Mit welcher horizontalen Kraft normal zur Triebwerksachse wirkt das Flugzeug auf den rotierenden Teil des Triebwerks ein? |
|||
#Wie gross ist das einwirkende Drehmoment? |
|||
#Die beiden Lager sind symmetrisch zum Schwerpunkt des rotierenden Teils im gegenseitigen Abstand von 1.8 m angeordnet. Mit welcher Kraft wird das vordere Lager bei diesem Flugmanöver belastet. Geben Sie die y- und z-Kraftkomponente bezüglich des folgenden Koordinatensystems an: |
|||
::''x'' in Flugrichtung |
|||
::''y'' gegen die Kurvenmitte |
|||
::''z'' nach unten. |
|||
'''[[Lösung zu Aviatik 2008/Ass|Lösung]]''' |
'''[[Lösung zu Aviatik 2008/Ass|Lösung]]''' |
||
Aktuelle Version vom 25. August 2010, 13:45 Uhr
Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung
Daten:
| Gravitationsfeldstärke g | 9.81 N/kg |
| universelle Gaskonstante R | 8.314 J/(mol K) |
| Dichte von Wasser | 1000 kg/m3 |
| spezifische Wärmekapazität von Wasser | 4.18 kJ/(kg K) |
| Anzahl Freiheitsgrade der Luftmolekülen | 5 |
| Anzahl Freiheitsgrade der Heliummolekülen | 3 |
Aufgabe 1
Ein Kondensator (Kapazität 4 mF oder 0.004 F), der auf eine Spannung von 5 V aufgeladen wurde, wird danach über einem Widerstandselement (Widerstand 150 Ω) entladen.
- Wie gross ist die Spannung über dem Kondensator eine Sekunde nach Schliessen des Schalters?
- Skizzieren Sie das Systemdiagramm (Flowchart) für dieses System. Schreiben Sie alle zur Modellierung notwendigen Gleichungen auf.
- Ergänzen Sie das Systemdiagramm so, dass die im Widerstand dissipierte Energie laufend berechnet wird.
- Nun wird der Widerstand durch eine ideale Spule (Induktivität 2 mH) ersetzt. Zeichnen Sie ein neues Systemdiagramm (ohne Energieberechnung) und schreiben Sie die notwendigen Gleichungen wiederum separat dazu.
Aufgabe 2
Ein Güterwagen A (Masse unbekannt) prallt ungebremst mit einer Geschwindigkeit von 3 m/s in einen zweiten Wagen B (Masse 40 t), der anfänglich ruht und dessen Räder gebremst sind. In den beiden Diagrammen finden Sie die Geschwindigkeit des Wagens B sowie die totale Impulsstromstärke zwischen den Wagen (totale Pufferkraft) in Funktion der Zeit.
- Wie gross ist die Reibungskraft auf den Wagen B zum Zeitpunkt 0.8 s?
- Wie weit verschiebt sich der Wagen B, bis er wieder still steht?
- Wie viel Impuls fliesst durch die Puffer bis die Wagen gleich schnell sind? Wie gross ist die Masse des Wagens A?
- Wie viel Energie wird in den ersten 0.3 Sekunden infolge Reibung zwischen Schiene und Räder des Wagens B dissipiert?
-
v-t-Diagramm
-
F-t-Diagramm
Aufgabe 3
Im Schleudergang dreht sich die Trommel einer Waschmaschine (Durchmesser 40 cm) mit 1400 U/min (1400 RPM). Infolge einer Unachtsamkeit ist ein Fünffrankenstück (Masse 13,2 g) in die Maschine geraten und liegt nun direkt auf der Oberfläche der Trommel. Die Fragen beziehen sich auf einen Beobachter, der in der Waschküche steht.
- Zeichnen Sie alle Kräfte ein, die am höchsten Punkt der Kreisbahn auf das Geldstück einwirken. Geben Sie diesen Kräften einen passenden Namen.
- Berechnen Sie die Beschleunigung des Geldstücks beim höchsten Punkt der Bahn. In welche Richtung zeigt der Beschleunigungsvektor?
- Wie gross ist die Kraft der Trommel auf das Geldstück am höchsten und am tiefsten Punkt der Bahn? Geben Sie die Kraft als Vielfaches der Gewichtskraft an.
Aufgabe 4
Ein Turbofan (Eintrittsdurchmesser 1.6 m) erzeugt bei einer Luftdichte von 400 g/m3 und einer Geschwindigkeit des Flugzeugs von 250 m/s eine Schubkraft von 50 kN.
- Berechnen Sie die Stärke des durch das Triebwerk fliessenden Massenstroms und ermitteln Sie dann die Geschwindigkeit, mit der die Luft aus dem Triebwerk ausströmt. Idealisieren Sie dazu den Prozess, d.h. vernachlässigen Sie den Einfluss der Brennstoffzufuhr und nehmen Sie an, dass Kern- und Mantelstrom gleich schnell sind.
- Welche minimale Leistung würde dann (, wenn Kern- und Mantelstrom gleich schnell wären) das Triebwerk an den Luftstrom abgeben?
- Der Mantelstrom mache nun 80% des Luftstromes aus und trete halb so schnell wie der Kernstrom aus. Wie schnell tritt der Mantelstrom aus dem Triebwerk aus?
- Wie gross ist nun die minimale Leistung des Triebwerks?
Aufgabe 5
600 kg Wasser sollen von 15°C auf 75°C erwärmt werden. Dazu vergleichen wir drei verschiedene Möglichkeiten miteinander: Widerstandsheizung, Wärmepumpe mit festen Ein- und Ausgangstemperaturen, absolut reversibles Heizen.
- Wie gross ist der Energiebedarf, wenn diese Wassermenge mit einer elektrischen Widerstandsheizung aufgewärmt werden muss.
- Wie gross ist der Energiebedarf, wenn das Wasser mit Hilfe einer Wärmepumpe aufgeheizt wird? Die Wärme wird durch die Wärmepumpe reversibel von 0°C auf 90°C gefördert und fliesst von dort irreversibel ins aufzuheizende Wasser.
- Wie viel Entropie wird in diesem Fall zwischen der Wärmepumpe und dem aufzuheizenden Wasser erzeugt?
- Wie gross ist der Energiebedarf, wenn die Entropie der 27°C warmen Umgebung entnommenen und verlustfrei dem aufzuheizenden Wasser zugeführt wird?
Aufgabe 6
Der Stirling-Kreisprozess ist eine Idealisierung der in einem Stirling-Motor ablaufenden Vorgänge. Beim Stirling-Kreisprozess übernimmt ein Arbeitsgas Wärme bei konstanter Temperatur. Danach wird das Arbeitsgas isochor gekühlt, um dann im dritten Schritt Wärme isotherm abzugeben. Im vierten und letzten Teilprozess wird das Arbeitsgas isochor auf die ursprüngliche Temperatur erwärmt.
- Zeichnen Sie den Stirling-Kreisprozess im p-V-Diagramm und im T-S-Diagramm.
- Wie viel thermische Energie und wie viel Entropie nimmt ein Mol Helium bei 750 K auf, wenn sich das zugehörige Volumen von 1 Liter auf 3 Liter verdreifacht?
- Um welchen Wert ändert sich die innere Energie des Heliums, wenn es bei konstantem Volumen auf 300 K gekühlt wird?
- Weil das Arbeitsgas beim isochoren Abkühlen die Wärme an einen Zwischenspeicher abgibt und beim isochoren Aufheizen wieder von diesem bezieht, muss nur die zur isothermen Expansion benötigte Wärme extern zugeführt werden. Berechnen Sie nun den Wirkungsgrad des Stirling-Kreisprozesses, d.h. das Verhältnis zwischen nutzbarer Nettoarbeit und extern zugeführter Energie. Für den Kreisprozess nehmen Sie die bei b) und c) genannten Werte für Gas, Temperatur und Volumen.
Aufgabe 7
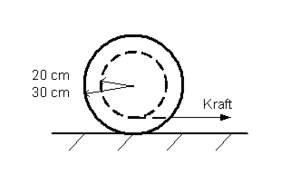
Auf eine ruhende Fadenspule (Masse 6 kg, Massenträgheitsmoment 0.1 kgm2, Abrollradius 30 cm, Wickelradius 20 cm) wirkt über einen horizontal ausgerichteten Faden eine Kraft ein. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N.
- Schneiden Sie die Fadenspule frei, d.h. zeichnen Sie alle Kräfte ein, die auf die Spule wirken und formulieren Sie die drei Bilanzgleichungen, die Grundgesetze der Mechanik.
- Mit welcher maximalen Kraft kann am Faden gezogen werden, damit die Spule gerade nicht rutscht?
- Wie gross ist dann die Beschleunigung der Spulenachse?
- In einem zweiten Versuch zieht man mit 20 N. Die Reibkraft beträgt immer noch 10 N. Wie gross ist nun die Beschleunigung der Spulenachse? Welchen Wert nimmt die Winkelbeschleunigung an?
Aufgabe 8
Ein Flugzeug fliegt mit einer Geschwindigkeit von 200 m/s durch eine horizontale Kurve (Radius 900 m). Der rotierende Teil des Turbojet-Strahltriebwerkes (Drehzahl 9000 U/min) hat eine Masse von 80 kg und weist ein Massenträgheitsmoment von 12 kgm2 auf.
- Mit welcher horizontalen Kraft normal zur Triebwerksachse wirkt das Flugzeug auf den rotierenden Teil des Triebwerks ein?
- Wie gross ist das einwirkende Drehmoment?
- Die beiden Lager sind symmetrisch zum Schwerpunkt des rotierenden Teils im gegenseitigen Abstand von 1.8 m angeordnet. Mit welcher Kraft wird das vordere Lager bei diesem Flugmanöver belastet. Geben Sie die y- und z-Kraftkomponente bezüglich des folgenden Koordinatensystems an:
- x in Flugrichtung
- y gegen die Kurvenmitte
- z nach unten.

