Widerstand und Auftrieb: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (48 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
*[[statischer Auftrieb]] |
*[[statischer Auftrieb]] |
||
*[[dynamischer Auftrieb]] |
*[[dynamischer Auftrieb]] |
||
*[[Luftwiderstand|Widerstand]] ( |
*[[Luftwiderstand|Widerstand]] (parasitärer und induzierter Widerstand) |
||
*Schub |
*Schub |
||
Luftschiffe und Ballone führen den gravitativ zufliessenden ''z''-Impuls als statischen Auftrieb an die umgebende Luft ab. Bei Objekten, die spezifisch viel schwerer sind als die Luft, wird dieser Auftrieb vernachlässigt bzw. direkt mit der Gewichtskraft verrechnet. Nachfolgend suchen wir nur eine brauchbare Beschreibung der einwirkenden Kräfte und fragen nicht, wieso ein Flugzeug überhaupt fliegt. |
Luftschiffe und Ballone führen den gravitativ zufliessenden ''z''-Impuls über ihre Oberfläche als statischen Auftrieb an die umgebende Luft ab. Bei Objekten, die spezifisch viel schwerer sind als die Luft, wird dieser Auftrieb vernachlässigt bzw. direkt mit der Gewichtskraft verrechnet. Nachfolgend suchen wir nur eine brauchbare Beschreibung der einwirkenden Kräfte und fragen nicht, wieso ein Flugzeug überhaupt fliegt. |
||
==Lernziele== |
==Lernziele== |
||
In dieser Vorlesung lernen Sie |
|||
*dass sowohl der statische als auch der dynamische Auftrieb aus der Druckverteilung an der Oberfläche des Körpers bestimmt werden kann |
|||
*wieso der statische Auftrieb gleich der Gewichtskraft der verdrängten Flüssigkeit oder des verdrängten Gases ist |
|||
*wie man den turbulenten Strömungswiderstand beschreibt |
|||
*dass die resultierende Kraft auf ein Flugzeug in Widerstand (parallel zur Anströmung) und Auftrieb (normal zur Anströmung) zerlegt werden kann |
|||
*dass sowohl der Widerstand als auch der Auftrieb proportional zum Quadrat der Anströmungsgeschwindigkeit und proportional zur Dichte der Luft sind |
|||
*wie der Strömungsbeiwert und der Auftriebsbeiwert definiert sind |
|||
==Strömungswiderstand== |
==Strömungswiderstand== |
||
===Potenzialströmung=== |
===Potenzialströmung=== |
||
[[Bild:Stroemung Kugel.jpg|thumb| |
[[Bild:Stroemung Kugel.jpg|thumb|Potenzialströmung und reale Strömung mit Ablösung]]Ein Körper, der reibungsfrei von einer [[Potenzialströmung]] umflossen wird, erfährt keine Strömungskraft (d'Alembertsches Paradoxon). Begründet wird dieses Paradoxon mit der Symmetrie der Strömung. Wohl staut sich das Fluid (Flüssigkeit oder Gas) an der Vorderseite des Körpers (vorderer Staupunkt), doch entsteht auf der Rückseite des umströmten Körpers ein zweiter Punkt, in dem die Strömungsgeschwindigkeit ebenfalls gleich Null ist (hinterer Staupunkt). Das d'Alembertsche Paradoxon, wonach der Strömungswiderstand (totale [[Impulsstrom]]stärke bezüglich der Körperoberfläche) verschwindet, beruht auf den sich kompensierenden Wirkungen der beiden Gebiete um den vorderen und hinteren Staupunkt. |
||
===laminare und turbulente Strömung=== |
===laminare und turbulente Strömung=== |
||
| Zeile 16: | Zeile 23: | ||
===einfaches Modell=== |
===einfaches Modell=== |
||
Die Grösse des Strömungswiderstandes bei turbulenter Umströmung kann mit Hilfe eines einfachen Modells abgeschätzt werden. Dazu stellen wir uns eine starre Scheibe (Fläche ''A'') vor, die normal stehend mit der Geschwindigkeit ''v'' gegen das Fluid bewegt wird. Vereinfachend machen wir folgende Annahmen |
[[Bild:Stroemungswiderstand2.png|thumb|Modell zur Bestimmung des Strömungswiderstandes]]Die Grösse des Strömungswiderstandes bei turbulenter Umströmung kann mit Hilfe eines einfachen Modells abgeschätzt werden. Dazu stellen wir uns eine starre Scheibe (Fläche ''A'') vor, die normal zur Anströmung stehend mit der Geschwindigkeit ''v'' gegen das Fluid bewegt wird. Vereinfachend machen wir folgende Annahmen |
||
*die sich einstellende Strömung ist eine [[Superposition]] aus |
*die sich einstellende Strömung ist eine [[Superposition]] aus Potenzialströmung und scharf berandetem turbulentem Nachlauf |
||
*der Querschnitt |
*der Querschnitt des turbulenten Nachlaufs ist gleich ''A'' |
||
*der Mittelwert über das Quadrat der Strömungsgeschwindigkeiten |
*der Mittelwert über das Quadrat der Strömungsgeschwindigkeiten im Nachlauf ist unmittelbar hinter der Scheibe gleich ''v<sup>2</sup>'' |
||
Zieht man nun diese Scheibe durch ein ruhendes Fluid, kann eine Leistungsbilanz aufgestellt werden. Die Leistung der Zugkraft (Kraft mal Geschwindigkeit)ist gleich der Änderungsrate der kinetischen Energie (Dichte der kinetischen Energie mal Änderungsrate des |
Zieht man nun diese Scheibe mit konstanter Geschwindigkeit durch ein ruhendes Fluid, kann eine Leistungsbilanz aufgestellt werden. Die [[Leistung einer Kraft|Leistung der Zugkraft]] (Kraft mal Geschwindigkeit) ist gleich der [[Änderungsrate]] der [[kinetische Energie|kinetischen Energie]] der Luft (Dichte der kinetischen Energie mal Änderungsrate des Nachlaufvolumens) |
||
:<math>P(F)=vF=\dot W_{kin}=\varrho_{kin}\dot V=\frac{1}{2}\rho v^2 A v</math> |
:<math>P(F)=vF=\dot W_{kin}=\varrho_{W{kin}}\dot V=\frac{1}{2}\rho v^2 A v</math> |
||
Bei gleichförmiger Bewegung der Scheibe ist die Zugkraft gleich dem gesuchten Strömungswiderstand. Also gilt |
Bei gleichförmiger Bewegung der Scheibe ist die Zugkraft gleich dem gesuchten Strömungswiderstand. Also gilt |
||
| Zeile 29: | Zeile 36: | ||
===reales Modell=== |
===reales Modell=== |
||
Der Querschnitt der Wirbelstrasse hängt von vielen Faktoren wie Form des umströmten Körpers oder Rauheit und Elastizität der Oberfläche ab. Zudem dürfte die Annahme, dass die Dichte der kinetischen [[Energie]] in der Wirbelstrasse im Mittel gleicht halbe Massendichte des Fluids mal das Quadrat der Anströmungsgeschwindigkeit ist, kaum zutreffen. Die dem einfachen Modell zugrunde liegende Annahme, dass der Strömungswiderstand proportional zur Dichte der kinetischen Energie der Anströmung und zum Querschnitt des umströmten Körpers zunimmt, ist durch Experimente vielfach bestätigt worden. Die verbleibende Unstimmigkeit wird nun in eine Zahl verpackt, die das Verhältnis zwischen Messung und einfachem Modell beschreibt. Diese Verhältniszahl nennt man [[Widerstandsbeiwert]]. |
|||
Der Strömungswiderstand lässt sich somit als Produkt aus Dichte der kinetischen Energie des anströmenden Fluids mal die um den Widerstandsbeiwert korrigierte Querschnittsfläche schreiben |
|||
:<math>F_W=\varrho_{W_{kin}}A_{korr}=\frac{1}{2}\varrho v^2 c_W A</math> |
|||
==statischer Auftrieb== |
==statischer Auftrieb== |
||
Der Auftrieb ist gleich dem Gewicht der verdrängten Flüssigkeit. Diesen Zusammenhang, der von ''Archimedes'' erstmals formuliert worden ist, kennt wohl jedes Kind. Doch wie kann eine Flüssigkeit, die verdrängt worden ist, noch eine Wirkung entfalten? Betrachten wir dazu einen Teich, auf dessen Grund ein Felsbrocken liegt. Würde man den Felsbrocken hoch heben, wäre die Hubkraft gleich der Gewichtskraft minus den Auftrieb. |
|||
In der [[Energiestrom und Prozessleistung|Vorlesung]] zur [[Hydrodynamik]] haben Sie den [[Druck]] als [[Energiebeladung]] des Volumenstroms kennen gelernt. Aus der Sicht der [[Translationsmechanik]] ist der Druck in ruhenden Gasen und Flüssigkeiten eine dreifache Impulsstromdichte. Der Druck besagt, wie viel ''x''-, ''y''- bzw. ''z''-Impuls pro Zeit und pro Fläche in ''x''-, ''y''- bzw. ''z''-Richtung transportiert wird. Befindet sich eine unter Druck stehende Flüssigkeit in einem Gefäss, muss jede Impulskomponente, die in der Flüssigkeit in ihre eigene Bezugsrichtung fliesst, von den Gefässwänden wieder zurück transportiert werden. Deshalb stehen Gefässwände immer unter Zugspannung. Nun führt das [[Gravitationsfeld]] der Flüssigkeit zusätzlich ''z''-Impuls zu (Quellendichte ''ρ g''). Weil die Flüssigkeit diesen [[Impuls]] nur vorwärts transportieren kann, nimmt die Impulsstromdichte infolge Zunahme der Quellen proportional mit der Eintauchtiefe zu |
|||
:<math>p=p_0+\varrho g z</math> |
|||
Um die Grösse der Auftriebskraft zu bestimmen, greifen wir einen beliebigen Teil des Wassers im Teich heraus und betrachten diesen Teil als Körper. Die Stärke der Impulsquelle heisst Gewichtskraft, die resultierende Druckkraft auf den ausgewählten Teil des Wassers nennt man Auftrieb. Weil der ausgewählte Körper natürlicherweise im Gleichgewicht ist, muss der Auftrieb gleich der Gewichtskraft sein. Ersetzt man nun das im ausgewählten Gebiet enthaltene Wasser durch einen gleich geformten Körper, ändert sich in der Regel das Gewicht. Die Druckverteilung an der Oberfläche und damit der Auftrieb bleibt dagegen gleich. Damit ist gezeigt, dass der '''Auftrieb gleich der Gewichtskraft der verdrängten Flüssigkeit''' ist. |
|||
Der Auftrieb kann auch direkt berechnet werden. Dazu muss man den Druck über die ganze Oberfläche des Körpers aufsummieren. Doch zuerst betrachten wir nur die Wirkung des Drucks auf ein kleines, ebenes Flächenstück. Zeigt die Flächennormale in ''x''-Richtung wirkt eine in ''x''-Richtung weisende Kraft auf das Flächenstück ein. Die Grösse dieser Kraft ist gleich Druck mal Fläche (Impulsstromstärke gleich Impulsstromdichte mal normal dazu stehende Fläche). Weitet man diese Betrachtung auf alle drei Impulskomponenten aus, erhält man die Kraft auf ein beliebig ausgerichtetes Flächenstück |
|||
:<math>\vec F=\begin{pmatrix} F_x\\F_y\\F_y\end{pmatrix}=p\begin{pmatrix} A_x\\A_y\\A_y\end{pmatrix}=p\vec A</math> |
|||
[[Bild:Auftriebskraft.gif|thumb|Druckkräfte auf prismatischen Körper]]Der Vektor '''''A''''' heisst Flächennormalvektor. Der Flächennormalvektor steht normal auf der Fläche und sein Betrag entspricht der Grösse der Fläche. Um die gesamte Druckkraft zu berechnen, muss die Oberfläche des Körpers in beliebig kleine Stücke der Grösse ''dA'' zerlegt werden. Danach berechnet man die Kraft auf jedes Stück und summiert über alle Stücke auf |
|||
:<math>\vec F_D=\int p\vec{dA}</math> |
|||
Die Oberfläche ist nach innen zu orientieren, damit das Integral der Auftriebskraft auf den Körper entspricht. Sind Körper und Flüssigkeit in Ruhe, kann der Druck durch die oben hergeleitete hydrostatische Formel ersetzt werden |
|||
:<math>\vec F_A=\int (p_0+\varrho g z)\vec{dA}=-\varrho g V\frac{\vec z}{z}</math> |
|||
Die zweite Umformung ist für einen prismatischen Körper trivial, im allgemeinen Fall aber nur unter Verwendung eines [[Satz von Gauss|Satzes von Gauss]] sauber durchzuführen. Wem diese Herleitung zu mathematisch ist, halte sich an die weiter oben gegebene Begründung mit dem ausgegrenzten Wasserkörper. |
|||
==dynamischer Auftrieb== |
==dynamischer Auftrieb== |
||
[[Bild:Polardiagramm LDP.gif|thumb|Polardiagramm der Beiwerte]]Ein Flugzeug fliegt, weil es den gravitativ zufliessenden ''z''-[[Impuls]] an die umgebende Luft abführen kann. Schneidet man die Triebwerke weg, erhält man an den Schnittflächen die Schubkräfte. Die Frage, wie die Triebwerke [[Impuls]] mit der Luft austauschen können, wird im Teil [[Impulsbilanz bei offenen Systemen]] beantwortet. Was für den statischen Auftrieb gilt, trifft auch auf den restlichen Teil der Flugzeughülle ziemlich gut zu: die Kraft der umgebenden Luft auf das Flugzeug ist gleich dem Integral über die Druckverteilung an der Flugzeugoberfläche |
|||
:<math>\vec F_{Luft}=\int p\vec{dA}</math> |
|||
In dieser Betrachtung fehlt die durch die vorbei strömende Luft verursachte Scherspannung (Dichte der querfliessenden Impulsströme). Die Wirkung dieses Teils des Impulsaustausches ist verglichen mit der Luftkraft zu vernachlässigen. Nun kann man zeigen, dass sich diese Luftkraft wie der weiter oben diskutierte Luftwiderstand verhält, aber infolge Bauweise und Stellung der Flügel eine Komponente normal zur Anströmung aufweist. Zerlegt man die Luftkraft bezüglich der Anströmung, erhält man den Widerstand (parallel zur Anströmung) und den dynamischen Auftrieb (normal zur Anströmung) |
|||
:<math>\vec F_{Luft}=\begin{pmatrix} F_A \\ F_W \end{pmatrix}=\frac{\varrho}{2}v^2\begin{pmatrix} c_A \\ c_W \end{pmatrix}A</math> |
|||
Als Fläche ''A'' nimmt man eine zu definierende Referenzfläche (Tragflügelfläche). Der Auftriebsbeiwert ''c<sub>A</sub>'' und der Widerstandsbeiwert ''c<sub>W</sub>'' enthalten die wesentliche Information zu den beiden Komponenten der Luftkraft. Da beide Beiwerte vom Anstellwinkel abhängen, muss die Lage des Flugzeuges gegen die Anströmung bekannt sein. Zur Veranschaulichung kann man die Beiwerte in Funkton des Anstellwinkels auftragen oder beide Beiwerte als Polardiagramm gegeneinander stellen. Im Polardiagramm erscheint der Anstellwinkel als Parameter auf der Kurve. |
|||
==Flugdynamik== |
|||
Sobald sich die Fluggeschwindigkeit der Schallgeschwindigkeit nährert, ändern sich die Strömungsverhältnisse grundlegend. Nachfolgend ein paar Überlegungen zur Ärodynamik des Flugzeuges im Unterschallbereich (subsonic flow regime). Dabei gehen wir immer von einer Gleichgewichtssituation bezüglich Translation und Rotation aus. Im Gleichgewicht ist die Summe über alle Kräfte (Summe über die Stärken der [[Impulsstrom|Impulsströme]] und [[Impulsquelle]]n) sowie die Summe über alle Drehmomente (Summe über die Stärken aller [[Drehimpulsstrom|Drehimpulsströme]] und [[Drehimpulsquelle]]n) gleich Null. Die Bewegung des Flugzeuges gegen die umgebende Luft (true air speed) bzw. die Anströmung der Luft gegen das Flugzeug bezeichnen wir als Geschwindigkeit. |
|||
===Segelflug=== |
|||
[[Bild:KraefteAufSegelflugzeug.png|thumb|Kräfte (rot) auf Segelflugzeug, Komponenten (blau) der Luftkraft]]Auf ein Segelflugzeug wirken nur das Gravitationsfeld und die umströmende Luft ein. Die Wirkung der umströmenden Luft kann bezüglich der Anströmung in einen Auftrieb (normal zur Anströmung) und einen Widerstand (parallel zur Anströmung) zerlegt werden. Weil die Gewichtskraft und die Gesamtkraft der Luft das Flugzeug im Gleichgewicht halten, gilt |
|||
:<math>F_G\cos(\gamma)=F_A=\frac{\varrho}{2}v^2c_A A</math> |
|||
:<math>F_G\sin(\gamma)=F_W=\frac{\varrho}{2}v^2c_W A</math> |
|||
Dividiert man die zweite Gleichungen durch die erste erhält man folgende Beziehung |
|||
:<math>\frac{F_G\sin(\gamma)}{F_G\cos(\gamma)}=\tan(\gamma)=\frac{F_W}{F_A}=\frac{c_W}{c_A}</math> |
|||
Im Polardiagramm misst man den Gleitwinkel ''γ'' als Winkel zwischen der Ordinate und der Verbindungslinie vom Koordinatenursprung zum aktuellen Punkt auf der Polaren. Die Tangente an die Polare liefert deshalb den kleinstmöglichen Gleitwinkel. Die zum gleichförmigen Gleiten notwendige Geschwindigkeit ergibt sich aus der oben formulierten Gleichgewichtsbedingung. |
|||
===Reiseflug=== |
|||
Im horizontalen Reiseflug ist der Gleitwinkel ''β'' gleich Null. Der Auftrieb sollte dann das Gewicht und der Schub den Widerstand kompensieren. Falls die Triebwerke dementsprechend ausgerichtet sind, gilt |
|||
:<math>F_S=F_W=\frac{\varrho}{2}v^2c_W A=\frac{c_W}{c_A}F_G</math> |
|||
Im Reiseflug ist das Flugzeug im Gleichgewicht. Dennoch meinen viele Leute, dass die Schubkraft grösser sein müsse als der Luftwiderstand. Dies hängt mit dem Energieumsatz zusammen. Ein Strahltriebwerk entzieht der durchströmenden Luft [[Impuls]]. Dieser Impuls fliesst über das Flugzeug an die umgebende Luft zurück. Der gesamte Impulsdurchsatz ist mit zwei Prozessen verbunden. Im ersten Prozess, der in den Triebwerken stattfindet, muss der Impuls von der durchströmenden Luft ins Flugzeug gepumpt werden. Im zweiten Prozess fliesst der Impuls unter Energiedissipation an die umgebende Luft zurück. Die dabei freigesetzte Prozessleistung ist gleich der Leistung der Luftwiderstandskraft, falls als [[Bezugssystem]] die umgebende Luft genommen wird |
|||
:<math>P=\Delta v I_p=P(F_W)=\frac{\varrho}{2}c_W A v^3</math> |
|||
Die in den Wirbelstrassen dissipierte Leistung steigt demnach mit der dritten Potenz der Geschwindigkeit. Eine ähnliche Gesetzmässigkeit findet man auch beim Autofahren. Wer mit 240 km/h über die Autobahn fährt, benötigt fast acht Mal mehr Leistung als bei einer Fahrt mit 120 km/h (bei der Autofahrt treten neben dem Luftwiderstand noch weitere Verlustleistungen auf, die zum Teil linear mit der Geschwindigkeit ansteigen). |
|||
== Kontrollfragen == |
== Kontrollfragen == |
||
#Der statische Auftrieb ist gleich dem Gewicht der verdrängten Flüssigkeit. Wie erklärt man diesen Sachverhalt? |
|||
*Wie |
|||
#Wie berechnet man den statischen Auftrieb bei bekanntem Volumen und gegebener Dichte des Fluids? |
|||
#Wie geht die Anströmungsgeschwindigkeit in die Berechnung von Widerstand und dynamischen Auftrieb ein? |
|||
#Wie bestimmt man den kleinstmöglichen Gleitwinkel aus dem Polardiagramm (Auftriebsbeiwert gegen Widerstandsbeiwert)? |
|||
#Wie fliesst der Vertikalimpuls im Reiseflug durch das Flugzeug hindurch? Wie nennt man die beiden zugehörigen Impulsstrom- bzw. Impulsquellenstärken? |
|||
#Wie fliesst der Horizontalimpuls im Reiseflug durch das Flugzeug hindurch? Wie nennt man die beiden zugehörigen Impulsstromstärken? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Denkt man sich den eingetauchten Körper aus einem Stoff mit der gleichen Dichte wie die umgebende Flüssigkeit geschaffen, würde der Körper frei schweben. Die Auftriebskraft (resultierende Druckkraft) ist dann gleich der Gewichtskraft. Unterscheidet sich nun die Dichte des Körpers von der umgebenden Flüssigkeit, ändert sich das Gewicht nicht aber der Auftrieb. |
|||
#Der statische Auftrieb ist gleich der Gewichtskraft auf die vom Körper verdrängte Flüssigkeit <math>F_A=\varrho_{fl}gV</math>. |
|||
#Widerstand und dynamischer Auftrieb nehmen mit dem Quadrat der Anströmgeschwindigkeit zu. |
|||
#Der kleinstmögliche Gleitwinkel ergibt sich durch die Tangente an die Kurve im Polardiagramm. |
|||
#Orientiert man die ''z''-Achse gegen unten, fliesst vom Gravitaionsfeld ein konstanter ''z''-Impulsstrom zu (Gewichtskraft). Damit das Flugzeug nicht abstürzt, muss dieser Impuls über die Luft abgeführt werden (dynamischer Auftrieb). |
|||
#Orientiert man die ''x''-Achse in Flugrichtung, fliesst ein geschwindigkeitsabhängiger ''x''-Impulsstrom an die Luft weg (Luftwiderstand). Damit das Flugzeug seine Geschwindigkeit beibehält, müssen die Triebwerke diesen Verlust ausgleichen (Schubkräfte). |
|||
| ⚫ | |||
*[https://cast.switch.ch/vod/clips/y0srolsdx/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=bQQqhjKi5bc Kurzfassung auf Youtube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik 2014]]''' |
|||
| ⚫ | |||
*[[Physik - Ein systemdynamischer Zugang für die Sekundarstufe II]] Seiten 110 - 111 |
|||
'''[[Physik und Systemwissenschaft in Aviatik |
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
||
[[Kategorie:VorAV]] |
[[Kategorie:VorAV]] |
||
Aktuelle Version vom 26. November 2015, 17:22 Uhr
Fliegende Körper tauschen mit dem Gravitationsfeld und der umgebenden Luft Impuls aus. Die Stärke des quellenartigen Impulsaustausches mit dem Gravitationsfeld nennt man Gewichtskraft. Der Impulsaustausch mit der Luft wird in verschiedene Kräfte aufgespalten:
- statischer Auftrieb
- dynamischer Auftrieb
- Widerstand (parasitärer und induzierter Widerstand)
- Schub
Luftschiffe und Ballone führen den gravitativ zufliessenden z-Impuls über ihre Oberfläche als statischen Auftrieb an die umgebende Luft ab. Bei Objekten, die spezifisch viel schwerer sind als die Luft, wird dieser Auftrieb vernachlässigt bzw. direkt mit der Gewichtskraft verrechnet. Nachfolgend suchen wir nur eine brauchbare Beschreibung der einwirkenden Kräfte und fragen nicht, wieso ein Flugzeug überhaupt fliegt.
Lernziele
In dieser Vorlesung lernen Sie
- dass sowohl der statische als auch der dynamische Auftrieb aus der Druckverteilung an der Oberfläche des Körpers bestimmt werden kann
- wieso der statische Auftrieb gleich der Gewichtskraft der verdrängten Flüssigkeit oder des verdrängten Gases ist
- wie man den turbulenten Strömungswiderstand beschreibt
- dass die resultierende Kraft auf ein Flugzeug in Widerstand (parallel zur Anströmung) und Auftrieb (normal zur Anströmung) zerlegt werden kann
- dass sowohl der Widerstand als auch der Auftrieb proportional zum Quadrat der Anströmungsgeschwindigkeit und proportional zur Dichte der Luft sind
- wie der Strömungsbeiwert und der Auftriebsbeiwert definiert sind
Strömungswiderstand
Potenzialströmung
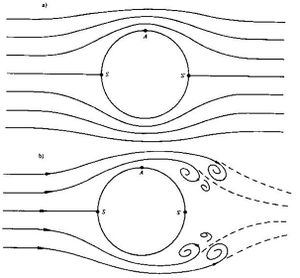
Ein Körper, der reibungsfrei von einer Potenzialströmung umflossen wird, erfährt keine Strömungskraft (d'Alembertsches Paradoxon). Begründet wird dieses Paradoxon mit der Symmetrie der Strömung. Wohl staut sich das Fluid (Flüssigkeit oder Gas) an der Vorderseite des Körpers (vorderer Staupunkt), doch entsteht auf der Rückseite des umströmten Körpers ein zweiter Punkt, in dem die Strömungsgeschwindigkeit ebenfalls gleich Null ist (hinterer Staupunkt). Das d'Alembertsche Paradoxon, wonach der Strömungswiderstand (totale Impulsstromstärke bezüglich der Körperoberfläche) verschwindet, beruht auf den sich kompensierenden Wirkungen der beiden Gebiete um den vorderen und hinteren Staupunkt.
laminare und turbulente Strömung
Ein reales Fluid wirkt infolge der eigenen Zähigkeit (Viskosität) mit Scherkräften (querfliessende Impulsströme) auf den umströmten Körper ein. Bei Newtonschen Flüssigkeiten nimmt der durch die Zähigkeit verursachte Impulsaustausch zwischen Fluid und Körper linear mit der Anströmungsgeschwindigkeit zu. Überschreitet die Scherbelastung in der Flüssigkeit eine gewisse Grenze, lösen sich erste Grenzschichten ab. Die sich vom Körper ablösenden Grenzschichten bilden hinter dem Körper eine turbulente Wirbelstrasse. Der Unterdruck im Gebiet der Wirbelstrasse ist die eigentliche Ursache für den Strömungswiderstand bei turbulenter Umströmung.
einfaches Modell
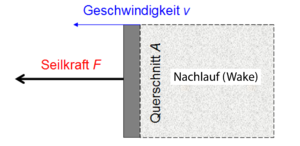
Die Grösse des Strömungswiderstandes bei turbulenter Umströmung kann mit Hilfe eines einfachen Modells abgeschätzt werden. Dazu stellen wir uns eine starre Scheibe (Fläche A) vor, die normal zur Anströmung stehend mit der Geschwindigkeit v gegen das Fluid bewegt wird. Vereinfachend machen wir folgende Annahmen
- die sich einstellende Strömung ist eine Superposition aus Potenzialströmung und scharf berandetem turbulentem Nachlauf
- der Querschnitt des turbulenten Nachlaufs ist gleich A
- der Mittelwert über das Quadrat der Strömungsgeschwindigkeiten im Nachlauf ist unmittelbar hinter der Scheibe gleich v2
Zieht man nun diese Scheibe mit konstanter Geschwindigkeit durch ein ruhendes Fluid, kann eine Leistungsbilanz aufgestellt werden. Die Leistung der Zugkraft (Kraft mal Geschwindigkeit) ist gleich der Änderungsrate der kinetischen Energie der Luft (Dichte der kinetischen Energie mal Änderungsrate des Nachlaufvolumens)
- [math]P(F)=vF=\dot W_{kin}=\varrho_{W{kin}}\dot V=\frac{1}{2}\rho v^2 A v[/math]
Bei gleichförmiger Bewegung der Scheibe ist die Zugkraft gleich dem gesuchten Strömungswiderstand. Also gilt
- [math]F_W=\frac{1}{2}\rho v^2 A[/math]
reales Modell
Der Querschnitt der Wirbelstrasse hängt von vielen Faktoren wie Form des umströmten Körpers oder Rauheit und Elastizität der Oberfläche ab. Zudem dürfte die Annahme, dass die Dichte der kinetischen Energie in der Wirbelstrasse im Mittel gleicht halbe Massendichte des Fluids mal das Quadrat der Anströmungsgeschwindigkeit ist, kaum zutreffen. Die dem einfachen Modell zugrunde liegende Annahme, dass der Strömungswiderstand proportional zur Dichte der kinetischen Energie der Anströmung und zum Querschnitt des umströmten Körpers zunimmt, ist durch Experimente vielfach bestätigt worden. Die verbleibende Unstimmigkeit wird nun in eine Zahl verpackt, die das Verhältnis zwischen Messung und einfachem Modell beschreibt. Diese Verhältniszahl nennt man Widerstandsbeiwert.
Der Strömungswiderstand lässt sich somit als Produkt aus Dichte der kinetischen Energie des anströmenden Fluids mal die um den Widerstandsbeiwert korrigierte Querschnittsfläche schreiben
- [math]F_W=\varrho_{W_{kin}}A_{korr}=\frac{1}{2}\varrho v^2 c_W A[/math]
statischer Auftrieb
Der Auftrieb ist gleich dem Gewicht der verdrängten Flüssigkeit. Diesen Zusammenhang, der von Archimedes erstmals formuliert worden ist, kennt wohl jedes Kind. Doch wie kann eine Flüssigkeit, die verdrängt worden ist, noch eine Wirkung entfalten? Betrachten wir dazu einen Teich, auf dessen Grund ein Felsbrocken liegt. Würde man den Felsbrocken hoch heben, wäre die Hubkraft gleich der Gewichtskraft minus den Auftrieb.
In der Vorlesung zur Hydrodynamik haben Sie den Druck als Energiebeladung des Volumenstroms kennen gelernt. Aus der Sicht der Translationsmechanik ist der Druck in ruhenden Gasen und Flüssigkeiten eine dreifache Impulsstromdichte. Der Druck besagt, wie viel x-, y- bzw. z-Impuls pro Zeit und pro Fläche in x-, y- bzw. z-Richtung transportiert wird. Befindet sich eine unter Druck stehende Flüssigkeit in einem Gefäss, muss jede Impulskomponente, die in der Flüssigkeit in ihre eigene Bezugsrichtung fliesst, von den Gefässwänden wieder zurück transportiert werden. Deshalb stehen Gefässwände immer unter Zugspannung. Nun führt das Gravitationsfeld der Flüssigkeit zusätzlich z-Impuls zu (Quellendichte ρ g). Weil die Flüssigkeit diesen Impuls nur vorwärts transportieren kann, nimmt die Impulsstromdichte infolge Zunahme der Quellen proportional mit der Eintauchtiefe zu
- [math]p=p_0+\varrho g z[/math]
Um die Grösse der Auftriebskraft zu bestimmen, greifen wir einen beliebigen Teil des Wassers im Teich heraus und betrachten diesen Teil als Körper. Die Stärke der Impulsquelle heisst Gewichtskraft, die resultierende Druckkraft auf den ausgewählten Teil des Wassers nennt man Auftrieb. Weil der ausgewählte Körper natürlicherweise im Gleichgewicht ist, muss der Auftrieb gleich der Gewichtskraft sein. Ersetzt man nun das im ausgewählten Gebiet enthaltene Wasser durch einen gleich geformten Körper, ändert sich in der Regel das Gewicht. Die Druckverteilung an der Oberfläche und damit der Auftrieb bleibt dagegen gleich. Damit ist gezeigt, dass der Auftrieb gleich der Gewichtskraft der verdrängten Flüssigkeit ist.
Der Auftrieb kann auch direkt berechnet werden. Dazu muss man den Druck über die ganze Oberfläche des Körpers aufsummieren. Doch zuerst betrachten wir nur die Wirkung des Drucks auf ein kleines, ebenes Flächenstück. Zeigt die Flächennormale in x-Richtung wirkt eine in x-Richtung weisende Kraft auf das Flächenstück ein. Die Grösse dieser Kraft ist gleich Druck mal Fläche (Impulsstromstärke gleich Impulsstromdichte mal normal dazu stehende Fläche). Weitet man diese Betrachtung auf alle drei Impulskomponenten aus, erhält man die Kraft auf ein beliebig ausgerichtetes Flächenstück
- [math]\vec F=\begin{pmatrix} F_x\\F_y\\F_y\end{pmatrix}=p\begin{pmatrix} A_x\\A_y\\A_y\end{pmatrix}=p\vec A[/math]
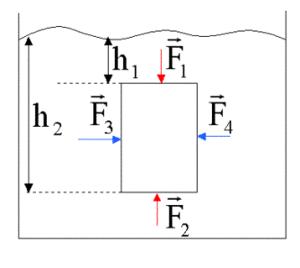
Der Vektor A heisst Flächennormalvektor. Der Flächennormalvektor steht normal auf der Fläche und sein Betrag entspricht der Grösse der Fläche. Um die gesamte Druckkraft zu berechnen, muss die Oberfläche des Körpers in beliebig kleine Stücke der Grösse dA zerlegt werden. Danach berechnet man die Kraft auf jedes Stück und summiert über alle Stücke auf
- [math]\vec F_D=\int p\vec{dA}[/math]
Die Oberfläche ist nach innen zu orientieren, damit das Integral der Auftriebskraft auf den Körper entspricht. Sind Körper und Flüssigkeit in Ruhe, kann der Druck durch die oben hergeleitete hydrostatische Formel ersetzt werden
- [math]\vec F_A=\int (p_0+\varrho g z)\vec{dA}=-\varrho g V\frac{\vec z}{z}[/math]
Die zweite Umformung ist für einen prismatischen Körper trivial, im allgemeinen Fall aber nur unter Verwendung eines Satzes von Gauss sauber durchzuführen. Wem diese Herleitung zu mathematisch ist, halte sich an die weiter oben gegebene Begründung mit dem ausgegrenzten Wasserkörper.
dynamischer Auftrieb
Ein Flugzeug fliegt, weil es den gravitativ zufliessenden z-Impuls an die umgebende Luft abführen kann. Schneidet man die Triebwerke weg, erhält man an den Schnittflächen die Schubkräfte. Die Frage, wie die Triebwerke Impuls mit der Luft austauschen können, wird im Teil Impulsbilanz bei offenen Systemen beantwortet. Was für den statischen Auftrieb gilt, trifft auch auf den restlichen Teil der Flugzeughülle ziemlich gut zu: die Kraft der umgebenden Luft auf das Flugzeug ist gleich dem Integral über die Druckverteilung an der Flugzeugoberfläche
- [math]\vec F_{Luft}=\int p\vec{dA}[/math]
In dieser Betrachtung fehlt die durch die vorbei strömende Luft verursachte Scherspannung (Dichte der querfliessenden Impulsströme). Die Wirkung dieses Teils des Impulsaustausches ist verglichen mit der Luftkraft zu vernachlässigen. Nun kann man zeigen, dass sich diese Luftkraft wie der weiter oben diskutierte Luftwiderstand verhält, aber infolge Bauweise und Stellung der Flügel eine Komponente normal zur Anströmung aufweist. Zerlegt man die Luftkraft bezüglich der Anströmung, erhält man den Widerstand (parallel zur Anströmung) und den dynamischen Auftrieb (normal zur Anströmung)
- [math]\vec F_{Luft}=\begin{pmatrix} F_A \\ F_W \end{pmatrix}=\frac{\varrho}{2}v^2\begin{pmatrix} c_A \\ c_W \end{pmatrix}A[/math]
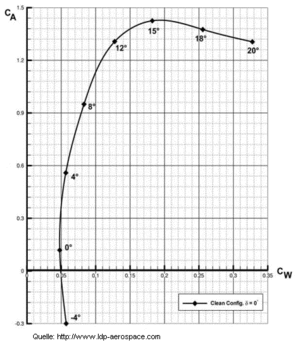
Als Fläche A nimmt man eine zu definierende Referenzfläche (Tragflügelfläche). Der Auftriebsbeiwert cA und der Widerstandsbeiwert cW enthalten die wesentliche Information zu den beiden Komponenten der Luftkraft. Da beide Beiwerte vom Anstellwinkel abhängen, muss die Lage des Flugzeuges gegen die Anströmung bekannt sein. Zur Veranschaulichung kann man die Beiwerte in Funkton des Anstellwinkels auftragen oder beide Beiwerte als Polardiagramm gegeneinander stellen. Im Polardiagramm erscheint der Anstellwinkel als Parameter auf der Kurve.
Flugdynamik
Sobald sich die Fluggeschwindigkeit der Schallgeschwindigkeit nährert, ändern sich die Strömungsverhältnisse grundlegend. Nachfolgend ein paar Überlegungen zur Ärodynamik des Flugzeuges im Unterschallbereich (subsonic flow regime). Dabei gehen wir immer von einer Gleichgewichtssituation bezüglich Translation und Rotation aus. Im Gleichgewicht ist die Summe über alle Kräfte (Summe über die Stärken der Impulsströme und Impulsquellen) sowie die Summe über alle Drehmomente (Summe über die Stärken aller Drehimpulsströme und Drehimpulsquellen) gleich Null. Die Bewegung des Flugzeuges gegen die umgebende Luft (true air speed) bzw. die Anströmung der Luft gegen das Flugzeug bezeichnen wir als Geschwindigkeit.
Segelflug
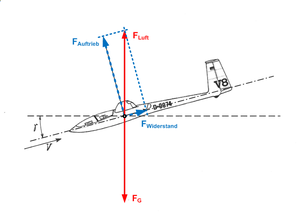
Auf ein Segelflugzeug wirken nur das Gravitationsfeld und die umströmende Luft ein. Die Wirkung der umströmenden Luft kann bezüglich der Anströmung in einen Auftrieb (normal zur Anströmung) und einen Widerstand (parallel zur Anströmung) zerlegt werden. Weil die Gewichtskraft und die Gesamtkraft der Luft das Flugzeug im Gleichgewicht halten, gilt
- [math]F_G\cos(\gamma)=F_A=\frac{\varrho}{2}v^2c_A A[/math]
- [math]F_G\sin(\gamma)=F_W=\frac{\varrho}{2}v^2c_W A[/math]
Dividiert man die zweite Gleichungen durch die erste erhält man folgende Beziehung
- [math]\frac{F_G\sin(\gamma)}{F_G\cos(\gamma)}=\tan(\gamma)=\frac{F_W}{F_A}=\frac{c_W}{c_A}[/math]
Im Polardiagramm misst man den Gleitwinkel γ als Winkel zwischen der Ordinate und der Verbindungslinie vom Koordinatenursprung zum aktuellen Punkt auf der Polaren. Die Tangente an die Polare liefert deshalb den kleinstmöglichen Gleitwinkel. Die zum gleichförmigen Gleiten notwendige Geschwindigkeit ergibt sich aus der oben formulierten Gleichgewichtsbedingung.
Reiseflug
Im horizontalen Reiseflug ist der Gleitwinkel β gleich Null. Der Auftrieb sollte dann das Gewicht und der Schub den Widerstand kompensieren. Falls die Triebwerke dementsprechend ausgerichtet sind, gilt
- [math]F_S=F_W=\frac{\varrho}{2}v^2c_W A=\frac{c_W}{c_A}F_G[/math]
Im Reiseflug ist das Flugzeug im Gleichgewicht. Dennoch meinen viele Leute, dass die Schubkraft grösser sein müsse als der Luftwiderstand. Dies hängt mit dem Energieumsatz zusammen. Ein Strahltriebwerk entzieht der durchströmenden Luft Impuls. Dieser Impuls fliesst über das Flugzeug an die umgebende Luft zurück. Der gesamte Impulsdurchsatz ist mit zwei Prozessen verbunden. Im ersten Prozess, der in den Triebwerken stattfindet, muss der Impuls von der durchströmenden Luft ins Flugzeug gepumpt werden. Im zweiten Prozess fliesst der Impuls unter Energiedissipation an die umgebende Luft zurück. Die dabei freigesetzte Prozessleistung ist gleich der Leistung der Luftwiderstandskraft, falls als Bezugssystem die umgebende Luft genommen wird
- [math]P=\Delta v I_p=P(F_W)=\frac{\varrho}{2}c_W A v^3[/math]
Die in den Wirbelstrassen dissipierte Leistung steigt demnach mit der dritten Potenz der Geschwindigkeit. Eine ähnliche Gesetzmässigkeit findet man auch beim Autofahren. Wer mit 240 km/h über die Autobahn fährt, benötigt fast acht Mal mehr Leistung als bei einer Fahrt mit 120 km/h (bei der Autofahrt treten neben dem Luftwiderstand noch weitere Verlustleistungen auf, die zum Teil linear mit der Geschwindigkeit ansteigen).
Kontrollfragen
- Der statische Auftrieb ist gleich dem Gewicht der verdrängten Flüssigkeit. Wie erklärt man diesen Sachverhalt?
- Wie berechnet man den statischen Auftrieb bei bekanntem Volumen und gegebener Dichte des Fluids?
- Wie geht die Anströmungsgeschwindigkeit in die Berechnung von Widerstand und dynamischen Auftrieb ein?
- Wie bestimmt man den kleinstmöglichen Gleitwinkel aus dem Polardiagramm (Auftriebsbeiwert gegen Widerstandsbeiwert)?
- Wie fliesst der Vertikalimpuls im Reiseflug durch das Flugzeug hindurch? Wie nennt man die beiden zugehörigen Impulsstrom- bzw. Impulsquellenstärken?
- Wie fliesst der Horizontalimpuls im Reiseflug durch das Flugzeug hindurch? Wie nennt man die beiden zugehörigen Impulsstromstärken?
Antworten zu den Kontrollfragen
- Denkt man sich den eingetauchten Körper aus einem Stoff mit der gleichen Dichte wie die umgebende Flüssigkeit geschaffen, würde der Körper frei schweben. Die Auftriebskraft (resultierende Druckkraft) ist dann gleich der Gewichtskraft. Unterscheidet sich nun die Dichte des Körpers von der umgebenden Flüssigkeit, ändert sich das Gewicht nicht aber der Auftrieb.
- Der statische Auftrieb ist gleich der Gewichtskraft auf die vom Körper verdrängte Flüssigkeit [math]F_A=\varrho_{fl}gV[/math].
- Widerstand und dynamischer Auftrieb nehmen mit dem Quadrat der Anströmgeschwindigkeit zu.
- Der kleinstmögliche Gleitwinkel ergibt sich durch die Tangente an die Kurve im Polardiagramm.
- Orientiert man die z-Achse gegen unten, fliesst vom Gravitaionsfeld ein konstanter z-Impulsstrom zu (Gewichtskraft). Damit das Flugzeug nicht abstürzt, muss dieser Impuls über die Luft abgeführt werden (dynamischer Auftrieb).
- Orientiert man die x-Achse in Flugrichtung, fliesst ein geschwindigkeitsabhängiger x-Impulsstrom an die Luft weg (Luftwiderstand). Damit das Flugzeug seine Geschwindigkeit beibehält, müssen die Triebwerke diesen Verlust ausgleichen (Schubkräfte).