Flüssigkeitsbild
Das Bild
Im Flüssigkeitsbild werden dynamische Vorgänge durch hydraulisch äquivalente Prozesse veranschaulicht. Das hier vorgeschlagene Bild enthält alle Zusammenhänge, die für das Verständnis eines systemdynamischen Modells relevant sind.
Im Flüssigkeitsbild wird ein homogene System (Körper, Schwungrad, Kondensator oder Wärmespeicher) zu einem Gefäss, das in einem riesigen See steht. Die Gefässe verhalten sich kapazitiv, die Verbindungen zwischen den Gefässen gehorchen resistiven oder induktiven Gesetzen. Der See steht für die Erde, mit der jedes System unbeschränkt Flüssigkeit (Impuls, Drehimpuls, elektrische Ladung oder Entropie) austauschen kann. Denkt man sich die Dichte der Flüssigkeit und die Gravitationsfeldstärke gleich eins, wird die Grundfläche der Gefässe zur Kapaztität (Masse, Massenträgheitsmoment, Kapazität oder Entropiekapazität) und die Füllhöhe zum Potenzial (Geschwindigkeit, Winkelgeschwindigkeit, elektrisches Potzenzial oder Temperatur ).
Das Flüssigkeitsbild eignet sich bestens zur Darstellung von Vorgängen aus der Translations- und der Rotationsmechanik. In der Elektrizitätslehre überträgt man nur den halben Kondensator als echten Speicher ins Flüssigkeitsbild. Die Entropieproduktion setzt der Anwendung des Flüssigkeitsbildes in der Thermodynamik gewisse Grenzen. Beschränkt man sich dabei auf reversible Prozesse wie ideale Wärmekraftmaschinen, Wärmepumpen oder homogene Wärmespeicher, stellt das Flüssigkeitsbild die Prozessleistung, den zugeordneten Energiestromes oder die Wärmekapazität korrekt dar. Bei total irreversiblen Prozessen könnte man auch die Energie als Flüssigkeit nehmen und damit thermischen RC-Gliedern untersuchen. Nur geht dann ein beträchtlicher Teil der Aussagekraft des Flüssigkeitsbildes verloren.
Die einzelnen Grössen werden wie folgt ins Flüssigkeitsbild übertragen:
| Flüssigkeitsbild | Translation | Rotation | Elektrizität | Wärme |
|---|---|---|---|---|
| Flüssigkeitsmenge | Impuls | Drehimpuls | Ladung | Entropie |
| Gefässquerschnitt | Masse | Massenträgheitsmoment | elektrische Kapazität | Entropiekapazität |
| Füllhöhe | Geschwindigkeit | Winkelgeschwindigkeit | elektrisches Potenzial | absolute Temperatur |
| Fallhöhe | Geschwindigkeitsdifferenz | Winkelgeschwindigkeitsdifferenz | Spannung | Temperaturdifferenz |
Translation
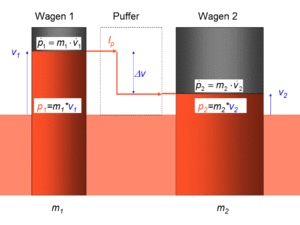
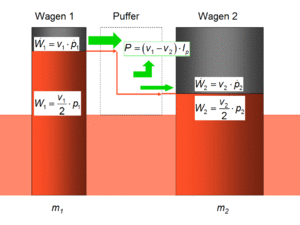
Der Auflaufstoss eines Güterwagens gegen einen zweiten eignet sich bestens, um die Aussagekraft des Flüssigkeitsbildes zu illustrieren. Die beiden Güterwagen werden als zwei zylindrische Gefässe mit der Masse als zugehörige Grundfläche dargestellt. Anfänglich ist das eine Gefäss gefüllt und das andere leer. Durch die Wirkung der Puffer fliesst der Impuls (Flüssigkeit) vom auflaufenden Wagen (Gefäss) in den ruhenden über. Bis sich die Geschwindigkeiten (Füllhöhen) angeglichen haben, setzt der Impulsstrom in den Puffern Energie frei. Am Schluss dieser Phase I sind die Puffer voll eingefahren. In der zweiten Phase pumpen die Puffer zusätzlich Impuls unter Energieabgabe vom Hammer- in den Ambosswagen. Die Beschleunigung erscheint im Flüssigkeitsbild als Steig- oder Sinkgeschwindigkeit des Flüssigkeitsspiegels.
Aus dem Flüssigkeitsbild können folgende Informationen mehr oder weniger direkt entnommen werden:
- Impulsinhalt = Masse*Geschwindigkeit
- Impulsübertrag = Masse*Geschwindigkeitsänderung
- mittlere Impulsstromstärke = Impulsübertrag durch benötigte Zeit
- Impulsänderungsrate = Summe über alle Impulsströme
- Beschleunigung = Impulsänderungsrate durch Masse
- Prozessleistung = Impulsstromstärke*aktuelle Geschwindigkeitsdifferenz
- zugeordneter Energiestrom = Impulsstromstärke mal aktuelle Geschwindigkeit
- Energieumsatz = Impulsübertrag*mittlere Geschwindigkeitsdifferenz (Phase I: Impuls fliesst hinunter; Phase II: Impuls fliesst hinauf)
- kinetische Energie = Impulsinhalt*halbe Geschwindigkeit (Die kinetische Energie wird freigesetzt, wenn der gesamte Impuls an die Erde abfliesst)
Die gemeinsame Geschwindigkeit der Wagen am Schluss von Phase I nennt man Geschwindigkeit des Massenmittelpunktes beider Wagen. Phase I heisst auch inelastischer Stoss. Indem man die vom Impuls in der Phase II von den Puffern aufgenommene Energie mit der in Phase I freigesetzten vergleicht, erhält man ein Mass für die Elastizität des Stosses (Stosszahl).