Mechanische Energieströme
Die Physik der dynamischen Systeme unterscheidet zwischen zugeordnetem Energiestrom und Prozessleistung. Der zugeordnete Energiestrom tritt meist im Zusammenhang mit der Bilanz bezüglich eines Systems auf. Wenn ein Strom eine Potenzialdifferenz durchfällt oder über eine solche gepumpt werden muss, wird Energie im Sinne einer Prozessleistung umgesetzt. Die Prozessleistung beschreibt also den Energieumsatz pro Zeit. Prozessleistung und zugeordneter Energiestrom werden nicht in allen Zweigen der Physik gleichermassen untersucht. Bei elektrischen Stromkreisen verwendet man meist nur den Begriff Prozessleistung (P = UI ). In der Thermodynamik wird praktische nur mit dem Begriff des zugeordneten Energiestromes (Wärmestrom) argumentiert.
Die Mechanik lässt sich nicht so einfach in das allgemeine Schema der systemdynamischen Analyse pressen. Dafür sind mehrere Gründe verantwortlich. Die Mechanik kennt sechs skalare bilanzierfähige Mengen, nämlich den Impuls und den Drehimpuls mit je drei Komponenten ("Sorten"). Diese Mengen können leitungsartig (stromartig) und quellenartig transportiert werden. Zudem ist die Mechanik in ihren Anfängen als reine Bewegungslehre ohne Bezug zu irgendwelchen Prozessen formuliert worden. Die Begriffe Prozessleistung und zugeordneter Energiestrom lassen sich aber problemlos auf die Mechanik übertragen.
Translation
Ein Drahtseil, das quer über einen Waldweg gezogen wird, transportiert Impuls und Energie. Indem wir nur ein Stück Seil betrachten, können wir sofort sagen, auf welcher Seite sich die Seilwinde befindet und auf welcher Seite der Baum befestigt ist. Durch das gespannte und bewegte Seil fliesst ein Impulsstrom und ein Energiestrom. Orientiert man die x-Achse längs des Seils, strömt der x-Impuls mit einer bestimmten Stärke in negative Richtung. Die Geschwindigkeit des Seils ordnet dann diesem Impulsstrom einen Energiestrom zu: der Impuls ist das Energieträger und die Geschwindigkeit das zugehörige Beladungsmass. Die Richtung des zugeordneten Energiestromes hängt im Gegensatz zur Richtung des Impulsstromes nicht von der Wahl des Koordinatensysems ab, weil sich sowohl das Vorzeichen der Menge (Impuls) als auch des Potenzials (Geschwindigkeit) mit dem Umdefinieren der positiven Richtung ändert
- [math]I_W = v_x I_{px}[/math]
Diese Formel gilt streng genommen nur bezüglich einer orientierten Referenzfläche, d.h. man muss einen bestimmten Querschnitt des Seils auswählen und dieser Fläche eine positive Richtung zuordnen. Die positive Richtung wird oft mit einem Bezugspfeil markiert. Fliesst nun der Impuls in positive Richtung, wird dessen Stromstärke mit einem Wert grösser Null angegeben. Bewegt sich das Seil ebenfalls in positive Richtung, ist die Geschwindigkeit grösser Null und die Stärke des Energiestromes wird mit einem Wert grössser Null angegeben.

Spannt man einen Expander und denkt sich die Bezugsrichtung parallel zu den Gummiseilen, fliesst der Impuls im Expander in negative und im Brustkasten in positive Richtung. Streckt man den einen Arm weiter aus, wird der Impulsstrom in den aktiven Muskeln mit Energie beladen
- [math]P = \Delta v_x I_{px}[/math]
Dieselbe Prozessleistung setzt der Impulsstrom im Expander wieder frei. Ein vergleichbarer Prozess läuft beim Polieren von Schuhen ab. Steckt man die linke Hand in den Schuh und hält mit der rechten die Bürste fest, erzeugt man beim Polieren ein Impuls-Wechselstrom. Unabhängig von der Wahl der Bezugsrichtung fliesst die Energie stossweise aus den Muskeln in die zu polierende Oberfläche.
Im Gegensatz zu einem elektrischen Stromkreisen spielen bei einem mechanischen die Kapazitäten (Massen) eine grössere Rolle. Deshalb eignen sich stationäre Prozesse besser, um den Zusammenhang zwischen Impuls- und Energiestrom zu erklären. Ein schönes Beispiel findet man beim Velo (Fahrrad, ursprünglich Veloziped für Schnellfuss). Zeigt die positive Richtung nach vorn, fliesst in der belasteten Kette der Impuls nach hinten. Der zugehörige Impulskreis ist über den Rahmen kurzgeschlossen. Der Impulsstrom wird im vorderen Zahnkranz mit Energie beladen, transportiert diese dann über die Kette gegen deren Bewegungsrichtung nach hinten und setzt sie im hinteren Zahnkranz wieder frei. Ohne Reibung wäre die Prozessleistung im hinteren Zahnrad entgegengesetzt gleich gross wie im vorderen.

Der zugeordnete Energiestrom hängt im Gegensatz zur Prozessleistung von der Wahl des Potenzialnullpunktes, also von der Wahl des Beobachters, ab. Vom Velofahrer aus gesehen transportiert der Impulsstrom die Energie vom vorderen Zahnkranz durch die Kette zum hinteren. Ein aussenstehender Beobachter "sieht" eine andere Energiebeladung. Aus seiner Sicht fliesst in der Kette ein viel grösserer Energiestrom nach hinten (die Geschwindigkeit, das zugehörige Potenzial, ist für einen aussenstehenden Beobachter gleich Geschwindigkeit der Kette relativ zum Fahrrad plus Geschwindigkeit des Fahrrades). Weil der im Rahmen nach vorne fliessende Impulsstrom nun ebenfalls einen Energiestrom nach hinten transportiert (Geschwindigkeit des Fahrrades mal Impulsstromstärke), "sieht" der Zuschauer an der Tour de Suisse netto den gleichen Energiestrom vom Tretlager zur Hinterachse fliessen wie der mitfahrende Radprofi.
Die Prozessleistung ist unabhängig vom Beobachter. Enthält also ein System keine echten Speicher (Systeme, welche die Primärgrösse oder den Energieträger speichern) oder untersucht man nur stationäre Transportvorgänge, sollte man sich bei der Beschreibung der Energieumsätze wie bei elektrischen Stromkreisen auf die Prozessleistung beschränken.
Rotation
Ein zu einer Linksschraube verdrehter Stab transportiert den Drehimpuls vorwärts, in einer rechtsschraubig verformten Welle fliesst der Drehimpuls rückwärts. Diese Aussage ist unabhängig von der Wahl der positiven Drehrichtung. Eine verdrehte Welle transportiert aber erst Energie, wenn sie auch noch rotiert. Der zugeordnete Energiestrom ist dann gleich Winkelgeschwindigkeit mal Stärke des Drehimpulsstromes
- [math]I_W=\omega_x I_{L_x}[/math]
Falls der Drehimpuls von einem schnell drehenden in einen langsameren übergeht oder mittels eines Motors von einem Körper mit kleiner Winkelgeschwindigkeit in einen mit grösserer Drehzahl gepumpt wird, redet man von einem Prozess. Die Prozessleistung liefert dann die Beschreibung des Energieumsatzes pro Zeit
- [math]P=\Delta \omega_x I_{L_x}[/math]
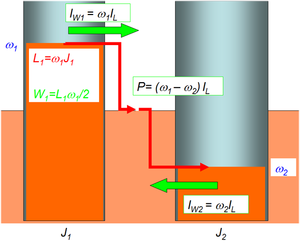
Werden zwei gegenläufig drehende Schwungräder über eine Rutschkupplung miteinander verbunden, fliesst der Drehimpuls vom Schwungrad mit der grösseren Winkelgeschwindigkeit ins andere Rad über (grösser und kleiner sind hier im Sinne der reellen Zahlen zu verstehen). Beim positiv drehenden Schwungrad fliesst die Energie mit dem Drehimpuls, beim negativ drehenden gegen den Drehimpulsstrom. Beide Energieströme fliessen demnach in die Rutschkopplung hinein. Dort ist die Prozessleistung gleich Differenz der beiden Winkelgeschwindigkeiten mal Stärke des durchfliessenden Drehimpulsstromes.
Analysiert man den Prozess im Flüssigkeitsbild, wird der Drehimpulsstrom zu einem Flüssigkeitsstrom (Massenstrom), der zugeordnete Energiestrom erscheint als Strom von potentieller Energie und die Prozessleistung bleibt Prozessleistung. Aus dem Flüssigkeitskeitsbild können weitere Zusammenhänge wie Drehimpulsinhalt gleich Massenträgheitsmoment mal Winkelgeschwindigkeit (Grundgläche mal Höhe) oder Rotationsenergie gleich Drehimpulsinhalt mal mittlere Winkelgeschwindigkeit entnommen werden. Zudem ist zu erkennen, dass der zugeordnete Energiestrom der Änderungsrate der Rotationsenergie entspricht.
Quellen
Das Gravitationsfeld bildet zusammen mit der Masse eine Impulsquelle bezüglich des Körpers. Die zugehörige Austauschrate kann nicht wie die Stärken der durch die Oberfläche eines Körpers fliessenden Impulsströme direkt gemessen werden. Die Stärke dieser Impulsquelle heisst Gewichtskraft
- [math]\vec F_G = m \vec g[/math]
Der gravitativen Impulsquelle wird in der Regel kein Energiestrom zugeordnet (die Gewichtskraft hat demnach keine Leistung). Folglich muss man die über das Gravitationsfeld ausgetauschte Energie dem Körper selber zuschreiben. Diese, ersatzweise dem Körper zugewiesene Energie heisst potentielle oder etwas konkreter Gravitationsenergie. Die Gravitationsenergie ist gleich Masse mal Gravitationspotenzial
- [math]W_G = m \varphi_G[/math]
Quellen treten nun auch beim Drehimpuls auf. Immer dann, wenn in einem Bauteil Impuls seitwärts zu seiner eigenen Bezugsrichtung fliesst, bildet sich gemäss des Hebelgesetzes eine Drehimpulsquelle. Dieser Drehimpulsquelle darf nun unter keinen Umständen ein Energiestrom zugeordnet werden.

In den Anfängen der Industrialisierung ist die Energie mechanisch von den Wasserwerken zu den mechanischen Werkstätten transportiert worden. Das Bild zeigt einen Teil der von Heinrich Moser (*1805 †1874) erbauten Transmissionsanlage in Schaffhausen. In den Stahlseilen wird die Energie vom durchfliessenden Impuls gegen die Bewegung des Seils transportiert. Dieser Impusstrom fliesst in den Rädern der Transmissionsanlage seitwärts zu seiner eigenen Bezugssrichtung und bildet dabei eine Quelle oder eine Senke des Drehimpulses. Der über die Quelle zufliessende Drehimpuls nimmt die vom Impulsstrom freigesetzte Energie auf und transportiert sie durch die Welle zum nächsten Rad. Dort verschwindet der Drehimpuls wieder aus unserem Gesichtsfeld und übergibt dabei die Energie an einen zweiten, ebenfalls quer fliessenden Impulsstrom. Dieses Beispiel zeigt, wieso man den Drehimpulsquellen keinen Energiestrom zuordnen darf. Der Drehimpuls quillt ins Rad hinein und übernimmt dabei die vom für die Quelle verantwortlichen, quer fliessenden Impuls freigesetzte Energie.
Leistung
Impuls und Drehimpuls können bezüglich eines raumfesten Koordinatensystems in sechs getrennt zu bilanzierende mengenartige Grössen unterteilt werden. Diese Mengen werden in den Bauteilen gespeichert, durch diese hindurch transportiert oder quellenartig mit der Umgebung ausgetauscht. Als siebte Menge wird dem ganzen Geschehen noch Energie überlagert, die ebenfalls gespeichert und transportiert werden kann.
Strombilder und Flüssigkeitsbilder liefern eine umfassende und überblickbare Beschreibung der Mechanik, falls die Dynamik vieler Bauteile analysiert werden muss und nur eine oder zwei Komponenten des Impulses oder des Drehimpulses eine wesentliche Rolle spielen. Kann ein System mit wenig Aufwand in einzelne Teile zerlegt werden, geht man mit Vorteil klassisch an die Analyse heran. Indem man die einzelnen Körper freischneidet, Grundgesetze sowie weitere Bedingungen formuliert, erhält man rasch einen vollständigen Satz von Differentialgleichungen. Aber auch für diese Vorgehensweise liefert die Physik der dynamischen Systeme eine saubere Grundlage.
Die Unterscheidung von Strömen und Quellen kann in die Formulierung der Grundgesetze übernommen werden, was eine gewisse Klarheit schafft
- [math]\sum_i \vec F_i + m \vec g = \dot {\vec p} = m \dot {\vec v}_{MMP}[/math]
- [math]\sum_j \vec M_j + \sum_k (\vec r_k \times \vec F_k) = \dot {\vec L}[/math]
Sowohl die Impuls- als Drehimpulsströme treten mehr oder weniger lokalisierbar über die Oberfläche des Körpers. Die Quellen (Gravitations- oder Gewichtskraft und Hebelgesetz) sind über das ganze Volumen des Körpers verteilt.
Multipliziert man die erste Gleichung skalar mit der Geschwindigkeit des Massenmittelpunktes und die zweite mit der Winkelgeschwindigkeit des fraglichen Körpers erhält man nach einer geometrischen Umformung die Leistungsbilanz bezüglich des starren Körpers
- [math]\sum_i (\vec F_i \cdot \vec v_i) + \sum_j (\vec M_j \cdot \vec \omega) = \sum_i P(\vec F_i) + \sum_j P(\vec M_j) = \dot {\vec p} \cdot {\vec v}_{MMP} - m \vec g \cdot {\vec v}_{MMP} + \dot {\vec L} \vec \omega = \dot W_{kin} + \dot W_G + \dot W_{rot}[/math]
Die Summe über die Leistungen aller Oberflächenkräfte (Skalarprodukt aus Kraft und Geschwindigkeit des "Angriffspunkts") und die Summe über die Leistungen aller reinen Drehmomente ist gleich der Summe über die Änderungsraten der kinetischen Energie, der Rotationsenergie und der Gravitationsenergie.
Integriert man die Leistungsbilanz über die Zeit, erhält man die erweiterte Form von dem was üblicherweise als Energiebilanz bezeichnet wird
- [math]\sum_i W(\vec F_i) + \sum_j W(\vec M_j) = \Delta W_{kin} + \Delta W_G + \Delta W_{rot}[/math]
Die Summe über die Arbeit der Oberflächenkräfte und die Summe über Arbeit der reinen Drehmomente ist gleich der Änderung der kinetischen Energie plus Änderung der Rotationsenergie plus Änderung der Gravitationsenergie.