Wärme als Entropie: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 180: | Zeile 180: | ||
:<math>P=(T_1-T_2)I_S</math> |
:<math>P=(T_1-T_2)I_S</math> |
||
Zur Illustration dieser Beziehung untersuchen wir die Wärmeströme bezüglich des Sekundärkreises eines Druckwasserreaktors. Im Verdampfer wird das Wasser unter hohem Druck und entsprechend hoher Temperatur verdampft. Der so erzeugt Dampf strömt danach durch eine Turbine und gibt dort Energie an den durch die Welle fliessenden [[Drehimpuls]] ab. Dabei kühlt sich der Dampf ab, d.h. manifeste Entropie geht in latente über. Neben der Temperatur wird auch der Druck kleiner. Im Kondensator gibt der Dampf so lange Entropie an den Kühlkreislauf ab, bis er ganz zu Wasser geworden ist. Danach bringt ein Pumpsystem das Wasser wieder auf den im Verdampfer herrschenden, hohen Druck. |
[[Bild:KKW mit DWR.png|thumb|[[Kernkraftwerk]] mit Druckwasserreaktor]]Zur Illustration dieser Beziehung untersuchen wir die Wärmeströme bezüglich des Sekundärkreises eines Druckwasserreaktors. Im Verdampfer wird das Wasser unter hohem Druck und entsprechend hoher Temperatur verdampft. Der so erzeugt Dampf strömt danach durch eine Turbine und gibt dort Energie an den durch die Welle fliessenden [[Drehimpuls]] ab. Dabei kühlt sich der Dampf ab, d.h. manifeste Entropie geht in latente über. Neben der Temperatur wird auch der Druck kleiner. Im Kondensator gibt der Dampf so lange Entropie an den Kühlkreislauf ab, bis er ganz zu Wasser geworden ist. Danach bringt ein Pumpsystem das Wasser wieder auf den im Verdampfer herrschenden, hohen Druck. |
||
Zum [[Kernkraftwerk|KKW]] Brokdorf findet man folgende Daten |
|||
Daten des Kernkraftwerks Brokdorf: |
|||
'''Primärkreis''' |
|||
{| |
|||
|width="320"|Betriebsdruck |
|||
|width="150"|157 bar (15,7 MPa) |
|||
|- |
|||
|Kühlmitteltemperatur beim Eintritt in Reaktor |
|||
|291.3 °C |
|||
|- |
|||
|Kühlmitteltemperatur beim Austritt aus Reaktor |
|||
|326.1 °C. |
|||
|- |
|||
|Kühlmittelstrom |
|||
|67680 t/h |
|||
|- |
|||
|Reaktorleistung |
|||
|3765 MW |
|||
|} |
|||
'''Sekundärkreis''' |
|||
{| |
|||
|width="250"|Temperperatur der Vorwärmanlage |
|||
|width="150"|218°C |
|||
|- |
|||
|Sattdampferzeugung |
|||
|2,061 t/s (285°/ 66 bar) |
|||
|- |
|||
|Generatorleistung |
|||
|1395 MW |
|||
|- |
|||
|Generatorspannung |
|||
|27 kV |
|||
|} |
|||
'''Kühlkreis''' |
|||
{| |
|||
|width="200"|Kühlmittelstrom |
|||
|208008 t/h |
|||
|- |
|||
|max. Wassertemperatur |
|||
|33°C |
|||
|} |
|||
==Kontrollfragen== |
==Kontrollfragen== |
||
Version vom 27. Dezember 2007, 07:33 Uhr
Wärme kann gespeichert und transportiert, aber auch erzeugt werden. Sucht man in der Physik nach einer Grösse, die auf diese Umschreibung zutrifft, stösst man auf die Entropie. Entropie ist das Fachwort für die Wärmemenge der Umgangssprache. Leider ist der Begriff Wärme Mitte des 19. Jahrhunderts im Zusammenhang mit dem ersten Hauptsatz der Thermodynamik anders definiert worden. Deshalb versteht in der Physik unter Wärme die Energie, die zusammen mit der Entropie über die Systemgrenze transportiert wird.
Entropie ist eine bilanzierbare Grösse der Physik. Zudem trägt jeder leitungsartige Entropiestrom einen (thermischen) Energiestrom über die Systemgrenze, wobei die absolute Temperatur das Energiebeladungsmass darstellt. Mikroskopisch macht sich die gespeicherte Entropie in einer Vergrösserung der Zustandssumme bemerkbar. Unter der Zustandssumme versteht man die Zahl der mikroskopischen Anordnungen, die im gleichen makroskopischen Zustand (Druck, Temperatur, Volumen, Stoffmenge, chemisches Potenzial) möglich sind.
Lernziele
Entropiespeicher
Entropie kann temperaturwirksam (manifest) oder ohne Temperaturveränderung (latent) gespeichert werden. Betrachten wir dazu ein Stück Eis, das in einem mit verschiebbaren Kolben verschlossenen Zylinder eingegossen ist. Der Kolben sorgt für einen konstanten Druck im Innern des Zylinders. Heizt man das System langsam auf, steigt die Temperatur des Eises kontinuierlich an. Bei 0°C bleibt die Temperatur trotz Wärmezufuhr über längere Zeit konstant. Dabei wandelt sich das Eis in Wasser um. Danach steigt die Temperatur wieder an, bis der Siedepunkt erreicht ist. Bei der Siedetemperatur, deren konkreter Wert stark vom herrschenden Druck abhängt, bleibt die Temperatur erneut stehen und das Wasser wandelt sich in Dampf (gasförmiger Zustand) um (das Wort Siedetemperatur ist hier irreführend, da man ein eigentliches Sieden nur beobachten würde, wenn die Umwandlung in einer offenen Pfanne stattfände). Schlussendlich steigt die Temperatur des Dampfes wieder konitnuierlich an.
Die oben geschilderten fünf Heizphasen können in zwei verschiedene Gruppen eingeteilt werden
- manifest: Speicherung von Entropie durch Temperaturanstieg von festen, flüssigen und gasförmigen Körpern
- latent: Speicherung von Entropie durch Umwandlung von fest in flüssig oder von flüssig in gasförmig
Gasförmige (und im beschränktem Umfang auch flüssige und feste) Stoffe können Entropie manifest und latent speichern
- manifest: Speicherung von Entropie durch Temperaturanstieg bei konstant gehaltenem Volumen
- latent: Speicherung von Entropie durch Volumenvergrösserung bei konstant gehaltener Temperatur
Auf der doppelten Speicherfähigkeit der Gase in Bezug auf die Entropie basieren die meisten Wärmekraftmaschinen und Wärmepumpen.
Gemischte Stoffe speichern mehr Entropie, als wenn sie bei sonst gleichem Zustand (Temperatur, Druck) nebeneinander gelagert würden. Mischentropie tritt auf, wenn
- sich zwei Gase (gleicher Druck, gleiche Temperatur) mischen
- Salz in Wasser gelöst wird
- Wasser in Luft verdunstet
Weil Entropie auch produziert werden kann, wird bei vielen Mischvorgängen die dazu notwendige Entropie direkt erzeugt. Beim Entmischen muss die Mischentropie, unabhängig ob sie vorher erzeugt oder zugeführt worden ist, abgeführt werden.
Impuls und Drehimpuls sind lange nicht als Primärgrössen der Physik wahrgenommen worden, weil wir diese Bewegungsmengen praktisch unbeschränkt der Erde entnehmen können. Mit der Entropie verhält es sich ähnlich. Erschwerend kommt hinzu, dass die Entropie in einem sich selbst überlassenen System, den unter den gegebenen Umständen maximalen Wert annehmen kann. Eine Grösse, die überall zu haben ist und sich zudem andauernd vermehrt, hat praktisch keinen Marktwert. Und dennoch wird die Zukunft unserer Zivilisation stark vom richtigen Umgang mit der Entropie abhängen.
zugeordneter Energiestrom
Wie in allen andern zweigen der Physik tritt die Energie auch in der Thermodynamik als reine Buchhaltungsgrösse auf. Dass in der Wärmelehre einzelne Sachverhalte statt mit der Entropie mit Energie erklärt werden, hängt zum Teil mit der historischen Entwicklung zusammen. Zudem Teil aber auch mit der Verlässlichkeit der thermischen Energie bei total irreversibeln Vorgängen. Mit diesen Aspekten wollen wir uns in späteren Vorlesungen auseinander setzten. Zuerst wollen wir uns aber mit der Bedeutung der Entropie als Energieträger auseinander setzen. In dieser Hinsicht lässt sich die Entropie ohne Einschränkung in das allgemeine Schema der Physik der dynamischen Systeme einordnen.
| Gebiet | Menge | Einheit | Potenzial | Einheit |
|---|---|---|---|---|
| Gravitation | Masse | kg | Gravitationspotenzial | J/kg |
| Hydrodynamik | Volumen | m3 | Druck | Pa |
| Elektrodynamik | elektrische Ladung | C, As | elektrisches Potenzial | J/C, V |
| Translationsmechanik | Impuls | Ns, kgm/s | Geschwindigkeit | m/s |
| Rotationsmechanik | Drehimpuls | Nms, kgm2/s | Winkelgeschwindigkeit | 1/s |
| Thermodynamik | Entropie | J/K | absolute Temperatur | K |
Dass bei der historischen Entwicklung der Thermodynamik etwas schief gelaufen ist, erkennt man schon bei den Einheiten. So wird die elektrische Ladung in Coulomb und das Potenzial in Joule pro Coulomb gemessen. In der Thermodynamik ist das Potenzial, die Temperatur, mit einer Basiseinheit versehen worden. Die eigentliche Primärgrösse, die Entropie, wird dann mit einer Einheit gemessen, die aus Energie und Temperatur gebildet worden ist.
Als Formelzeichen für die Entropie wird der Buchstabe S verwendet. Fliesst nun Wärme leitungsartig durch eine Referenzfläche der Temperatur T, kann dem Entropiestrom IS ein Energiestrom IW zugeordnet werden
- [math]I_W=T I_S[/math]
Oft wird die Stärke des thermischen Entropiestromes IW angegegeben. Dann kann die Stärke des Entropiestromes (gemessen in Watt pro Kelvin) mit Hilfe der absoluten Temperatur berechnet werden.
Prozessleistung
Die Vorstellung, dass ein Wärmestoff (Entropie) beim Hinunterfallen treibende Kraft (Energie) frei setzt, geht auf Sadi Carnot zurück. Weil Carnot bei seinen Überlegungen angenommen hat, dass die Entropie unter allen Umständen erhalten bleibt und treibende Kraft bei unsorgfälltigem Umgang verschwendet werden könne, konnten seine Ideen nicht ohne Widerspruch in eine tragfähige Grundlage der Thermodynamik umgearbeitet werden. Hätte er damals schon bemerkt, dass hinter der Verschwendung von treibender Kraft immer eine Wärmeproduktion steckt, wäre die Thermodynamik nicht so verknorzt formuliert worden.
Geht man von einer reversiblen Prozessführung aus, also von einem Prozess, bei dem keine Entropie erzeugt wird, trifft das von Carnot gezeichnete Bild voll zu. Fliesst Entropie von einem heissen Körper zu einem kalten, wird vom Wärmestrom die folgende Prozessleistung frei gesetzt
- [math]P=(T_1-T_2)I_S[/math]
Diese Prozessleistung kann nutzen, wer zwischen den beiden Körpern eine Wärmekraftmaschine laufen lässt. Mit dieser Formel reihen wir den thermischen Prozess in eine ganze Reihe von Elementarprozessen ein
- Graviationsprozess: die Masse des Wassers fliesst von einem Stausee in einen tiefer gelegenen See
- [math]P=g(h_1-h_2)I_m[/math]
- hydraulischer Prozess: das Volumen des Hydrauliköls strömt von einem Hochdruck- in einen Niederdruckbehälter
- [math]P=(p_1-p_2)I_V[/math]
- elektrischer Prozess: elektrische Ladung fliesst aus einem geladenen Kondensator in einen ungeladenen
- [math]P=(U_1-U_2)I[/math]
- translatorischer Prozess: Impuls fliesst von einem schnellen Fahrzeug in ein langsameres über
- [math]P=(v_{x_1}-v_{x_2})F_x[/math]
- rotatorischer Prozess: Drehimpuls strömt aus einem schnell drehenden Schwungrad in ein langsameres
- [math]P=(\omega_{x_1}-\omega_{x_2})M_x[/math]
- thermischer Porzess: Entropie fliesst aus einem heissen in ein kaltes System
- [math]P=(T_1-T_2)I_S[/math]
In diesem allgemeinen Schema fehlt noch ein letzter Prozess, mit dem wir uns aber in diesem Kurs nicht beschäftigen werden. Stoffmenge, die aus einem Gebiet mit hohem in ein Gebiet mit tiefem chemischen Potenzial strömt, setzt eine Prozessleistung frei, die ebenfalls gleich Potenzialdifferenz mal Stromstärke ist.
Entropieproduktion
In jedem Reibungsprozess wird Entropie produziert. Weil Entropie erzeugt, aber nicht vernichtet werden kann, liegt immer dann eine Reibungsprozess vor, wenn sich der Vorgang in der Zeit nicht umkehren lässt. In der Zeit umkehrbare Prozesse nennt man reversibel, nicht umkehrbare irreversibel. Die Entropieproduktion sorgt dafür, dass eine Zeitreise in die Vergangenheit nicht möglich ist.
reversible Vorgänge
Streng genommen sind exakt reversible Vorgänge nicht möglich, weil schon bei der Beobachtung (Messvorgang) eine minimale Entropiemenge produziert wird. Folgende Modelle verhalten sich im Prinzip reversibel, erzeugen also keine Entropie
- schiefer Wurf (nur eigentliche Bewegung ohne Abwurf oder Aufschlag)
- nicht gedämpfter Ein- oder Zweimassenschwinger
- physisches Pendel
- Bewegung der Himmelskörper
irreversible Prozesse
Ein irreversibler Prozess liegt vor, falls die im Prozess freigesetzte Leistung von keinem weiteren Prozess aufgenommen wird. Dann wird diese Prozessleistung auf die zu produzierende Entropie umgeladen. Geht man davon aus, dass die produzierte Entropie das Gebiet ihrer Entstehung (Temperatur T) in Form eines Wärmestromes verlässt, ist der weg fliessende Entropiestrom betragsmässig gleich der Produktionsrate
- [math]I_S+\Pi_S=0[/math]
Weil der dem Entropiestrom zugeordnete Energiestrom gleich der Prozesssleistung ist, gilt für die Produktionsrate der Entropie
- [math]\Pi_S=\frac{P_{diss}}{T}[/math]
Der Index diss soll darauf hinweisen, dass die Leistung dissipiert ist, dass die Energie für weitere Prozesse nicht mehr ohne weiteres zur Verfügung steht.
'Beispiele:
| Prozess | Leistung |
|---|---|
| Wasserfall | [math]P_{diss}=g(h_1-h_2)I_m[/math] |
| langes Rohr | [math]P_{diss}=(p_1-p_2)I_V[/math] |
| Widerstand | [math]P_{diss}=UI=RI^2=\frac{U^2}{R}[/math] |
| Knautschzone | [math]P_{diss}=(v_1-v_2)F[/math] |
| Rutschkupplung | [math]P_{diss}=(\omega_1-\omega_2)M[/math] |
| Wärmeleitung | [math]P_{diss}=(T_1-T_2)I_S[/math] |
Die Wärmeleitung nimmt eine gewisse Sonderstellung ein, weil im Primärprozess die gleiche Grösse "hinunter fällt" wie im Sekundärprozess produziert wird. Dabei muss zur Berechnung der Entropieproduktionsrate die tiefere Temperatur eingesetzt werden, weil die Wärme auf diesem Niveau weg fliesst.
Wärmepumpen
Eine Wärmepumpe fördert Wärme (Entropie) von einem System tiefer Temperatur (kaltes Wärmebad) in ein System hoher Temperatur (heisses Wärmebad). Eine Wärmepumpe kann zum Heizen oder Kühlen eines Gebäudes oder eines Raumes eingesetzt werden. Beim Heizen befindet sich der Nutzer auf der heissen Seite (Wärmepumpe gibt Entropie ab), beim Kühlen auf der kalten Seite(Wärmepumpe zieht Entropie ab).
Beispiel 1: Eine Wärmepumpe soll einen thermischen Energiestrom von 4 kW an 47°C warmes Wasser abgeben. Wie viel Prozessleistung muss sie mindestens aufnehmen, wenn sie Wärme aus dem 7°C warmen Grundwasser wegpumpt?
Lösung: In einem ersten Schritt berechnet man die Stromstärke der abzugebenden Entropie
- [math]I_S=\frac{I_W}{T_2}=\frac{4000 W}{320 K}[/math] = 12.5 W/K
Die minimale Prozessleistung (reversible Prozessführung) ist die dann gleich
- [math]P=(T_1-T_2)I_S=40K*12.5W/K[/math] = 500 W
Würde man die Entropie direkt mit Hilfe eines total irreversiblen Prozesses erzeugen, wäre die Prozessleistung gleich 4 kW.
Beispiel 2: Eine Kühltruhe (Innentemperatur -23°C) benötigt in 24 Stunden 1.2kWh elektrische Energie. Wie viel Wärmeenergie würde sie in dieser Zeit bei idealer Prozessführung über den Wärmetauscher an der Rückwand (Temperatur 47°C) abgeben?
Lösung: In 24 Stunden würde eine ideale Wärmepumpe die folgende Menge an Entropie fördern
- [math]S=\frac{W}{T_1-T_2}=\frac{4.32 MJ}{70 K}[/math] = 61.7 kJ/K
Diese Entropie trägt die folgende Energie
- [math]W_{therm}=ST_2=61.7kJ/K*320K[/math] = 19.7 MJ = 5.5 kWh
Ein Teil dieser Energie und auch der Entropie fliesst in diesen 24 Stunden im Kreis herum.
Wärmekraftmaschinen
Entropie, die aus einem System hoher Temperatur in ein kälteres überfliesst, besitzt ein Arbeitsvermögen, das von Wärmekraftmaschinen genutzt wird. Die dabei freigesetzte Prozessleistung berechnet sich nach der allgemeinen Formel
- [math]P=(T_1-T_2)I_S[/math]
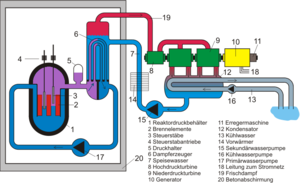
Zur Illustration dieser Beziehung untersuchen wir die Wärmeströme bezüglich des Sekundärkreises eines Druckwasserreaktors. Im Verdampfer wird das Wasser unter hohem Druck und entsprechend hoher Temperatur verdampft. Der so erzeugt Dampf strömt danach durch eine Turbine und gibt dort Energie an den durch die Welle fliessenden Drehimpuls ab. Dabei kühlt sich der Dampf ab, d.h. manifeste Entropie geht in latente über. Neben der Temperatur wird auch der Druck kleiner. Im Kondensator gibt der Dampf so lange Entropie an den Kühlkreislauf ab, bis er ganz zu Wasser geworden ist. Danach bringt ein Pumpsystem das Wasser wieder auf den im Verdampfer herrschenden, hohen Druck.
Zum KKW Brokdorf findet man folgende Daten Daten des Kernkraftwerks Brokdorf:
Primärkreis
| Betriebsdruck | 157 bar (15,7 MPa) |
| Kühlmitteltemperatur beim Eintritt in Reaktor | 291.3 °C |
| Kühlmitteltemperatur beim Austritt aus Reaktor | 326.1 °C. |
| Kühlmittelstrom | 67680 t/h |
| Reaktorleistung | 3765 MW |
Sekundärkreis
| Temperperatur der Vorwärmanlage | 218°C |
| Sattdampferzeugung | 2,061 t/s (285°/ 66 bar) |
| Generatorleistung | 1395 MW |
| Generatorspannung | 27 kV |
Kühlkreis
| Kühlmittelstrom | 208008 t/h |
| max. Wassertemperatur | 33°C |
Kontrollfragen
Materialien
- Skript Seiten 1 und 2
- Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 116 - 125