Basiskonzept

Das Basiskonzept der Physik der dynamischen Systeme ruht auf den drei Säulen Bilanz, konstitutive Gesetze und Rolle der Energie.

Bilanz

Für jede der sieben mengenartigen Grössen (Masse, Volumen, elektrische Ladung, Impuls, Drehimpuls, Entropie und Stoffmenge) kann bezüglich eines klar abgegrenzten Systems eine Bilanz formuliert werden. Die Bilanz besagt in ihrer einfachsten Form, dass die Summe über alle Stromstärken gleich der Änderungsrate des Inhalts ist

[math]\sum_i I_{M_i}=\dot M[/math]

Volumen, Entropie und Stoffmenge sind keine Erhaltungsgrössen. Nimmt eine dieser Mengen während des Austausches zu oder ab (Entropie kann nur zunehmen), muss die Bilanz durch eine Produktionsrate ergänzt werden

[math]\sum_i I_{M_i}+\Pi_M=\dot M[/math]

Impuls, Entropie und in einem gewissen Sinne auch Drehimpuls lassen sich konvektiv, leitungsartig sowie strahlungs- bzw. feldartig transportieren. Im letzten Fall tauscht das System die entsprechende Menge quellenartig aus. Damit erweitert sich die Bilanz zu

[math]\sum_i I_{M_i}+\sum_j I_{{M,con}_j}+\Sigma_M+\Pi_M=\dot M[/math]

Der griechische Buchstabe Sigma steht hier für Quellenstärke. Gibt das System die Menge über eine Quelle an die Umgebung ab, nimmt die Quellenstärke ein negatives Vorzeichen an und wird so zur Senke.

konstitutive Gesetze

Zu jeder mengenartigen Grösse lässt sich ein zugehöriges Potenzial angeben (Gravitationspotential, Druck, elektrisches Potential, Geschwindigkeit, Winkelgeschwindigkeit, absolute Temperatur und chemisches Potential). Die konstitutiven Gesetzt beschreiben ein spezielles Systemverhalten, indem sie eine Verbindung zwischen der Menge und dem Potenzial herstellen.

kapazitives Gesetz

Das kapazitive Gesetz liefert den Zusammenhang zwischen gespeicherter Menge und dem zugehörigen Potenzial eines homogenen Systems

[math]\varphi_M=f(M)[/math]

Dieser Zusammenhang nimmt bei einfachen Systemen oft die Form einer linearen Funktion an. Dann kann das Gesetz mit Hilfe einer Kapazität formuliert werden. Die Kapazität beschreibt das Verhältnis zwischen gespeicherter Menge und Änderung des zugehörigen Potenzials

[math]C_M=\frac{\Delta M}{\Delta \varphi_M}[/math]

Je mehr Menge pro Potenzialzunahme gespeichert werden kann, desto grösser ist die Kapazität. Der Begriff Kapazität darf auch bei nichtlinearem Zusammenhang verwendet werden. In diesem Fall ist die Kapazität differenziell zu definieren

[math]C_M(\varphi_M)=\frac{dM}{d\varphi_M}[/math]

Die Kapazität ist hier eine Funktion des Potenzials.

Beispiel: Die hydraulische Kapazität eines zylindrischen Gefässes ist gleich [math]C_V=\frac{\Delta V}{\Delta p}=\frac{A\Delta h}{\varrho g\Delta h}=\frac{A}{\varrho g}[/math]. Die Formel gilt auch für einen Stausee. Nur ist dort die Fläche eine Funktion der Füllhöhe oder des Drucks am Boden des Sees.

resistives Gesetz

Widerstände hindern den Strom am Fliessen

je grösser der Widerstand, desto grösser die anzulegende Potenzialdifferenz, damit der gleich Strom fliesst
je grösser der Widerstand, desto weniger Strom fliesst pro angelegter Potentialdifferenz hindurch

Fasst man diese beiden Eigenschaften zusammen, erhält man eine Definition für den Widerstand R_M

[math]R_M=\frac{\Delta\varphi_M}{I_M}[/math]

Diese Definition findet auch Anwendung, wenn der Widerstand nicht konstant ist. Bei grosser Nichtlinearität wird oft die Funktion [math]\Delta\varphi_M(I)[/math] bzw. die Kennlinie angegeben. Eine differentielle Formulierung des Widerstandes ist auch möglich, ergibt aber bei nichtlinearem Verhalten andere Werte die übliche Definition.

Beispiel: Strömt eine zähe Flüssigkeit laminar durch ein langes, dünnes Rohr, ist der Widerstand konstant. Bei weniger zähen Flüssigkeiten, dickeren Rohren und grösseren Strömungsgeschwindigkeiten wird die Strömung turbulent. Dann nimmt die Druckdifferenz über dem Rohr näherungsweise quadratisch mit der Volumenstromstärke zu. Der Strömungswiderstand selber ist dann eine lineare Funktion des Durchsatzes. Bei turbulenter Strömung verzichtet man häufig auf den Begriff Widerstand und wählt eine Beschreibung, bei welcher der Druckabfall mit dem Quadrat der Stromstärke verglichen wird.

induktives Gesetz

Induktives Verhalten tritt in der Hydrodynamik, der Mechanik und der Elektrodynamik auf. Die hydraulische Induktivität folgt aus der Trägheit der Flüssigkeit. Mechanischen Bauteile wie Zug-, Druck- und Torsionsfedern verhalten sich ebenfalls induktiv. Die elektrische Induktivität basiert auf dem Induktionsgesezt von Faraday, wonach die Änderungsrate des magnetischen Flusses eine umlaufende Spannung induziert.

Die Induktivität L_M beschreibt den Zusammenhang zwischen der angelegten Potenzialdifferenz und der Änderungsrate des durchfliessenden Stromes

[math]L_M=\frac{\Delta\varphi_M}{\dot I_M}[/math]

Bei einer Rohrleitung ist die hydraulische Induktivität gleich Dichte der Flüssigkeit mal Länge des Rohres geteilt durch Querschnitt. In der Translations- und der Rotationsmechanik entspricht die Induktivität dem Reziprokwert der Federkonstante. Die Induktivität einer Wicklung aus elektrisch leitendem Draht hängt von der Geometrie von der Beschaffenheit des Spulenkerns ab.

Das induktive Gesetz lässt sich auch nach der Stromstärke auflösen

[math]I_M=\int\frac{\Delta\varphi_M}{L_M}dt[/math]

Diese Darstellung wird hauptsächlich in der Mechanik verwendet, wobei man statt der Induktivität den zugehörigen Reziprokwert, die Federkonstante oder die Richtgrösse D, verwendet. Zudem ersetzt man die Zeit als frei Variable durch die Strecke oder den Winkel

[math]I_{px}=\int D(\Delta v_x)\Delta v_x dt=\int D(\Delta x) d(\Delta x)=D\Delta x[/math] oder [math]I_{Lx}=\int D^*(\Delta\omega_x)\Delta\omega_x dt=\int D^*(\Delta\varphi) d(\Delta\varphi)=D^*\Delta\varphi[/math]

Die jeweils letzte Umformung ist nur erlaubt, falls die Richtgrösse D oder die Winkelrichtgrösse D^* eine Konstante ist. Üblicherweise schreibt man statt Impulsstromstärke Kraft und statt Drehimpulsstromstärke Drehmoment, obwohl auf jede Feder zwei Kräfte bzw. zwei Drehmomente einwirken (eine Kraft ist eine Impulsstromstärke und ein Drehmoment eine Drehimpulsstromstärke bezüglich eines Systems).

Rolle der Energie

Die Energie ist eine reine Buchhaltungsgrösse, deren Bedeutung oft überschätzt wird. Nur bei einer Prozesskopplung oder einer Systemkopplung bildet die Energieerhaltung eine zusätzliche Randbedingung.

zugeordneter Energiestrom

Jedem leitungsartigen Mengenstrom (elektrischer Strom, Impulsstrom, Drehimpulsstrom, Entropiestrom) darf ein Energiestrom zugeordnet werden

[math]I_W=\varphi_MI _M[/math]

Die Potenziale heissen dann elektrisches Potenzial, Geschwindigkeit, Winkelgeschwindigkeit und absolute Temperatur. Diese Zuordnung gilt zudem für konvektive Ströme, indem man dem Volumenstrom über den Druck, dem Massenstrom über das Gravitationspotenzial und dem Stoffmengenstrom über das chemische Potenzial einen Energiestrom zuordnet.

Prozessleistung

Fliesst einer der oben erwähnten Ströme ungeschmälert durch ein System hindurch, setzt er eine Prozessleistung frei oder nimmt eine solche auf

[math]P=\Delta\varphi_M I_M[/math]

Im Gegensatz zum zugeordneten Energiestrom, der eine reine Buchhaltungsgrösse darstellt, handelt es sich bei der Prozessleistung um eine Leistung im landläufigen Sinne (Arbeitsvermögen pro Zeit). Die freigesetzte Prozessleistung kann auf einen zweiten Prozess übertragen werden. Man sagt dann, dass der erste Prozess den zweiten treibt. Geht ein Teil der Prozessleistung "verloren", wird damit Entropie erzeugt.

Systemdiagramm

Die hier skizzierte Struktur einer umfassenden Beschreibung elementarer Prozesse lässt sich direkt auf ein Systemdiagramm (graphischen Benutzeroberfläche eines systemdynamischen Werkzeuges) übertragen.

Bilanz

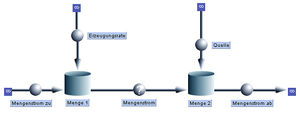
Die Systemdynamik basiert auf der Idee der Bilanz. Zeichnet man im Systemdiagramm (flowchart) einen Topf mit verschiedenen Zu- und Ableitungen, werden im Hintergrund die zugehörige Bilanz aufgestellt (die Summe über alle Stromstärken ist gleich der Änderungsrate des Inhalts), oabei Zuflüsse positiv und Abflüsse negativ gezählt werden. Bei der nachfolgenden Simulation wird dann die Änderungsrate über die Zeit integriert. Mathematisch gesehen bildet ein Topf mit einer einzelnen Zuleitung einen Integrator, welcher die Stromstärke über die Zeit integriert.

konstitutive Gesetze

Soll ein Speichergesetz ins Modell eingebaut werden, ist aus dem momentanen Zustand einer Topfgrösse das zugehörige Potential zu berechnen. Das Speichergesetz muss deshalb immer in der Form [math]\varphi_M=f(M)[/math] vorliegen.

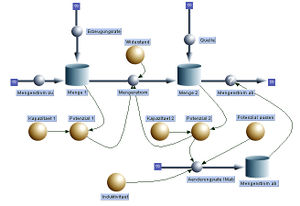
Widerstandsgesetze verbinden eine Potenzialdifferenz mit der Stärke eines Stromes. Auch hier ist die Kausalität gegeben. Zuerst müssen die Potenziale am Ein- und am Ausgang des Transportweges gegeben sein (explizit oder als Funktion einer Speichergrösse). Daraus ist dann die Stromstärke zu berechnen [math]I_M=f(\Delta\varphi)[/math]

Das induktive Gesetz ist ein wenig kontraintuitiv zu formulieren. Beim induktiven Verhalten bestimmt die Potenzialdifferenz die Änderungsrate der Stromstärke. Folglich ist ein Strom zu zeichnen, der eine Änderungsrate eines Stromes darstellt und in einen Topf mündet, der eine Stromstärke symbolisiert. Dieser Wert ist dann einer wahren Stromstärke im Hauptmodell zuzuordnen.

Geometrie

In der Mechanik treten neben den Mengen noch geometrische Zustandsgrössen auf (Ort und Drehwinkel). Diese Grössen sind wie der Impuls oder der Drehimpuls aus den Änderungsraten zu integrieren. Folglich zeichnet man für jede der drei Koordinaten einen Topf, der durch die jeweilige Geschwindigkeit gespiesen wird. Die Geschwindigkeit ergibt sich für alle drei Richtungen als Quotient von Impuls und Masse. In der Rotationsmechanik verfährt man anlaog. Im allgemeinen Fall bestimmt eine Komponente der Winkelgeschwindigkeit nicht nur die zugehörige Komponente des Drehwinkels. Zudem lässt sich die Winkelgeschwindigkeit nicht dirket durch eine einfache Division aus dem Drehimpuls berechnen.

Energie

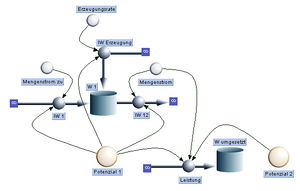
Zu jedem dynamischen Modell lässt sich eine Energiebilanz formulieren. Diese Bilanz hat jedoch keine Rückwirkung auf das dynamische Verhalten des Systems. Die Energiebilanz wird vielmehr vom dynamischen Modell mit Daten gefüttert. Das Systemdiagramm rechts zeigt einerseits einen Topf, der für die Energiebilanz bezüglich eines Systems (Menge 1) steht. Zu deren Formulierung ordnet man der Mengenbilanz einen zweiten Topf zu, der die Energie berechnet. Zusätzlich wird jedem Mengenstrom ein Energiestrom zugeordnet, wobei die Vorzeichenregel unbedingt zu übernehmen ist (zufliessende Mengenströme ergeben zufliessende Energieströme). Die Stärke eines jeden Energiestromes ist gleich Mengenstromstärke mal Potenzial des Systems.

Ausser der Energiebilanz kann auch noch die längs eines Transportweges umgesetzte Energie berechnet werden. Die umgesetzte Energie ist das Zeitintegral der Prozessleistung. Folglich bildet die umgesetzte Energie wie die Energie eines Systems eine Topfgrösse mit einem einzigen Zufluss, der Prozessleistung.

Links

Videoaufzeichnung zum Basiskonzept