Drehimpuls und Energie

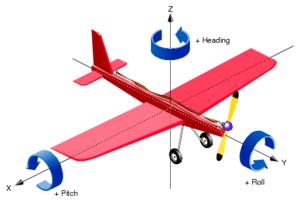
Ein starrer Körper kann sich in drei Richtungen bewegen und um drei normal zueinander stehende Achsen drehen. Nun besagt ein mathematischer Satz von Emmy Noether, dass zu jeder kontinuierlichen Symmetrie eines physikalischen Systems eine Erhaltungsgrösse gehört und umgekehrt. Die sechs Erhaltungsgrössen, die den kontinuierlichen Symmetrien Translation und Rotation entsprechen, sind die drei Komponenten des Impulses und des Drehimpulses.

Impuls und Drehimpuls sind nicht einfach nur Erhaltungsgrössen. Der Impuls, den man in der Umgangssprache Schwung oder Wucht nennt, ist die bilanzierfähige Basisgrösse der Translationsmechanik. Analog verhält es sich mit dem Drehimpuls. Der Drehimpuls ist genauso eine Primärmenge der Physik wie die Energie, die Masse, der Impuls, die elektrische Ladung oder die Entropie. Bezüglich eines raumfesten Koordinatensystems wird der Drehimpuls analog zum Impuls in drei getrennt zu bilanzierende Grössen aufgeteilt. In dieser Vorlesung wird die Rotationsmechanik anhand einer der drei Komponenten erklärt.

Lernziele

In dieser Vorlesung lernen Sie

dass der Drehimpuls die Primärgrösse der Rotationsmechanik ist
dass der Drehimpulsinhalt als Trägheitsmoment mal Winkelgeschwindigkeit geschrieben werden kann
dass ein in einer Antriebswelle vorwärts fliessender Drehimpuls diese zu einer Linksschraube verdreht
dass das Trägheitsmoment proportional mit der Masse zunimmt und von der Verteilung der Masse abhängt
dass die Winkelgeschwindigkeit als Energiebeladungsmass des Drehimpulses angesehen werden kann
dass die Rotationsenergie gleich Drehimpulsinhalt mal halbe Winkelgeschwindigkeit ist
dass sich viele Zusammenhänge der eindimensionalen Rotationsmechanik im Flüssigkeitsbild darstellen lassen
die Analogie zwischen Translations- und Rotationsmechanik kennen

Impuls

Der Impuls (Schwung oder Wucht) ist die Basismenge der Translationsmechanik. Der Impulsinhalt eines Körpers erzwingt die Geschwindigkeit von dessen Massenmittelpunkt. Der Zusammenhang zwischen Masse (Kapazität), Geschwindigkeit (Potenzial) und Impuls kann im Flüssigkeitsbild visualisiert werden.

Kombiniert man die Impulsbilanz (die Summe über alle Impulsstromstärken ist gleich Änderungsrate des Impulsinhaltes) mit dem kapazitiven Gesetz (Impulsinhalt gleich Masse mal Geschwindigkeit), erhält man das Grundgesetz der Mechanik

[math]\sum_i\vec F_i=\dot{\vec p}=m\dot{\vec v}[/math]

Eine Kraft ist demnach eine Impulsstromstärke bezüglich eines ausgewählten Körpers.

Drehimpuls

Impuls und Drehimpuls sind so alltägliche Grössen, dass wir uns ihrer gar nicht bewusst sind. Wir tauschen Impuls und Drehimpuls mit der Umgebung aus, sobald wir marschieren, Treppen steigen, Velo fahren oder schwimmen. Um den Drehimpuls kontrolliert zu untersuchen, lassen wir zwei Scheiben, die um eine vertikale Achse frei drehbar gelagert sind, gegeneinander rotieren. Zwischen den Scheiben befindet sich eine Spiralfeder, die mehr oder weniger stark gespannt werden kann.

Entsperrt man die Arretierung bei gespannter Feder, beginnen die beiden Scheiben gegenläufig zu rotieren. Die Erklärung dieses Vorgangs ist denkbar einfach. Sobald die Arretierung gelöst wird, pumpt die Feder Drehimpuls aus der einen Scheibe in die andere. Die Scheibe, die Drehimpuls abgibt, beginnt sich in negative Richtung zu drehen. Die Drehimpuls aufnehmende Scheibe dreht sich dann vorwärts. Wie beim Impuls muss das Vorzeichen geometrisch festgelegt werden. Dabei geht man nach der Regel der rechten Hand vor: falls der Daumen der rechten Hand in Richtung der Drehachse zeigt, geben die Finger die positive Drehrichtung an. Weist der Daumen nach oben und blickt man von oben auf das Gerät, ist der Gegenuhrzeigersinn positiv.
Setzt man danach die ober Scheibe auf die untere ab, stehen beide Körper nach kurzer Zeit wieder still. Die Reibung leitet Drehimpuls aus der einen Scheibe in die andere, bis sich die Winkelgeschwindigkeiten angeglichen haben.

Der gespeicherte Drehimpuls hängt wie der Impuls von zwei Faktoren ab, der Trägheit (Kapazität) und der "Füllhöhe" (Potenzial). Die Winkelgeschwindigkeit spielt hier die Rolle der Füllhöhe. Die Winkelgeschwindigkeit besagt, wie schnell sich ein Körper dreht. Zeichnet man eine beliebige Strecke auf die Oberfläche eines starren Körpers und misst den Winkel Δ φ, um den sich diese Linie in einem bestimmten Zeitabschnitt Δ t gedreht hat, ist die Winkelgeschwindigkeit ω gleich der Änderungsrate dieses Winkels

[math]\omega=\frac{\Delta \varphi}{\Delta t}[/math]

Die Winkelgeschwindigkeit wird in rad/s gemessen. Der Momentanwert der Winkelgeschwindigkeit wird aus der Winkel-Zeit-Funktion mittels einer Ableitung nach der Zeit gebildet. Die Winkelgeschwindigkeit ist die Änderungsrate des Drehwinkels

[math]\omega=\lim_{\Delta t \to 0}\frac{\Delta \varphi}{\Delta t}=\dot\varphi[/math]

Die Drehträgheit heisst offiziell Massenträgheitsmoment oder auch nur Trägheitsmoment J. Die Grösse des Trägheitsmoments hängt von der Masse und deren Verteilung ab.

Ersetzt man die eine Scheibe durch eine halb so dicke, rotiert sie nach der Einwirkung der Spiralfeder (minus) doppelt so schnell wie die andere. Dies ist zu erwarten, weil mit der Dicke auch die Masse halbiert wird.
Nimmt man eine Scheibe mit gleicher Masse, aber einem Radius, der Wurzel aus zwei mal kleiner ist, verdoppelt sich die Drehzahl ebenfalls. Das Massenträgheitsmoment einer Scheibe ist demnach proportional zur Masse und proportional zur Scheibenfläche.

Je weiter aussen sich die Masse befindet, desto träger wird ein Körper. Diese Eigenschaft lässt sich bei der Pirouette bestens studieren. Die auf der Spitze ihrer Schlittschuhe stehende Eiskunstläuferin ist bezüglich des Drehimpulses gegen Erde isoliert. Indem die Läuferin ihr Trägheitsmoment mit Hilfe der Arme und Beine verändert, vergrössert oder verkleinert sie ihre Winkelgeschwindigkeit.

Die Einheiten sind in der Rotationsmechanik ein leidiges Thema. Statt die Grundgrösse Drehimpuls mit einer eigenen Einheit zu versehen, werden alle Einheiten der Rotationsmechanik aus den Einheiten der Translationsmechanik abgeleitet. Deshalb wird das Massenträgheitsmoment in kgm² gemessen. Wenigstens sind die Einheiten so gewählt, dass der Drehimpulsinhalt L eines rotierenden Körpers direkt als Produkt aus Trägheitsmoment und Winkelgeschwindigkeit geschrieben werden kann

[math]L=J\omega[/math]

Der Drehimpuls wird folglich in kgm²/s gemessen. Im Karlsruher Physikkurs wird der Drehimpuls zu Ehren des Baslers Leonhard Euler in Euler (E) angegeben (1 E = 1kgm²/s).

Ströme und Bilanz

Impuls, der in seine eigene Bezugsrichtung durch einen Festkörper fliesst, erzeugt Druck. Fliesst der Impuls gegen seine Bezugsrichtung, steht das durchflossene Material unter Zug. Diesen Zusammenhang lässt sich bei der Eisenbahn sehr schön studieren. Strömt doch der Impuls bei einem Zug durch die Puffer vorwärts und durch die Zughaken rückwärts.

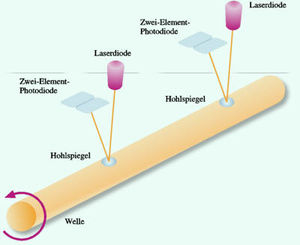
Flugzeuge tauschen dauernd über die Propeller Drehimpuls mit der umgebenden Luft aus. Dreht sich ein Propeller in positive Richtung, fliesst vom Motor her ein kontinuierlicher Drehimpulsstrom an die Luft weg. Diese speichert den aufgenommenen Drehimpuls, indem sie Wirbel bildet. Unter der Last des durchfliessenden Drehimpulses verdreht sich die Antriebswelle zu einer Linksschraube. Diese Regel gilt allgemein

Drehimpuls fliesst vorwärts - linksschraubige Verdrehung
Drehimpuls fliesst rückwärts - rechtsschraubige Verdrehung

Später werden wir diese Regel noch ausbauen müssen. Drehimpuls, der quer zu seiner Bezugsrichtung transportiert wird, belastet das durchflossene Bauteil auf Biegung.

Eine Kraft ist eine Impulsstromstärke bezüglich eines vorher ausgewählten Systems. In Analogie dazu wird Stärke eines Drehimpulsstromes bezüglich eines ausgewählten Systems als Drehmoment bezeichnet. Da ein Drehmoment in Newtonmeter (Nm) gemessen wird, darf der Drehimpuls auch in Newtonmetersekunde (Nms) angegeben werden.

Rotiert ein Körper um eine feste Achse, nimmt die Drehimpulsbilanz eine zur Impulsbilanz analoge Gestalt an

[math]\sum_i M_i=\dot L=J\dot \omega[/math]

Die Änderungsrate der Winkelgeschwindigkeit nennt man auch Winkelbeschleunigung.

Energie

Die Winkelgeschwindigkeit legt fest, wie stark ein rotierender Körper mit Drehimpuls "gefüllt" ist. Die Winkelgeschwindigkeit ist zudem das Energiebeladungsmass des Drehimpulsstromes, d.h. die Winkelgeschwindigkeit ordnet jedem Drehimpulsstrom einen Energiestrom zu. Der zugeordnete Energiestrom ist folglich gleich Winkelgeschwindigkeit mal Stärke des Drehimpulsstromes

[math]I_W=\omega I_L[/math]

Die Energie fliesst gegen den Drehimpuls, sobald sich eine Antriebswelle in negative Richtung dreht. Wendet man die Formel auf einen ausgewählten Körper an, nennt man die Stärke des Drehimpulsstromes Drehmoment und der zugeordnete Energiestrom wird zur Leistung dieses Drehmoments. Die Leistung eines Drehmoments ist demnach gleich Drehmoment mal Winkelgeschwindigkeit der Angriffsfläche

[math]P(M)=M\omega[/math]

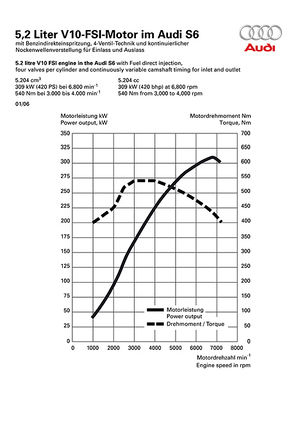
Um die Leistung eines Motors zu messen, wird die Antriebswelle gebremst. Aus Drehmoment und Drehzahl (Umdrehung pro Minute) lässt sich dann die Leistung berechnen. Im Drehmoment-Drehzahl-Diagramm ist die Leistung als Rechteckfläche (ein Punkt im Ursprung, der gegenüberliegende Punkt auf der Kurve) erkennbar.

Durchfliesst ein Drehimpulsstrom eine Rutschkupplung, wird eine Prozessleistung freigesetzt. Diese Leistung ist gleich der Differenz der beiden zugeordneten Energieströme, also gleich

[math]P=\Delta \omega I_L[/math]

Der Senkrechtstarter Osprey liefert ein schönes Beispiel für diese Prozessleistung. Weil die beiden Rotoren gegeneinander drehen, pumpt der eine Drehimpuls aus der Luft und der andere gibt den entsprechenden Drehimpulsstrom an die Luft zurück. Dabei muss der eine Motor den Drehimpuls vom sich in negative Richtung drehenden Rotor auf das Niveau des Senkrechtstarters (Winkelgeschwindigkeit gleich Null) pumpen. Der andere Motor fördert dann den gleichen Strom von Null auf die Winkelgeschwindigkeit des andern Rotors. Dank der Symmetrie der ganzen Anordnung sind sowohl die Drehimpulsströme als auch die "Pumphöhen" gleich gross. Würde einer der beiden Motoren ausfallen, wäre die Bilanz nicht mehr ausgeglichen und der Osprey würde zu rotieren anfangen.

Die Energie, die zusammen mit dem Drehimpuls gespeichert ist, heisst Rotationsenergie. Analog zur kinetischen Energie ist die Rotationsenergie gleich Drehimpuls mal halbe Winkelgeschwindigkeit

[math]W_{rot}=\frac{\omega}{2}L=\frac {J}{2}\omega^2=\frac {L^2}{2 J}[/math]

Die Rotationsenergie wird freigesetzt, falls der Körper bei festem Trägheitsmoment zum Stillstand kommt. Je nach anfänglicher Drehrichtung setzt dann der gegen das Bezugssystem abfliessende (positive Drehrichtung) oder der von dort zufliessende Drehimpuls (negative Drehrichtung) diese Energie frei.

Flüssigkeitsbild

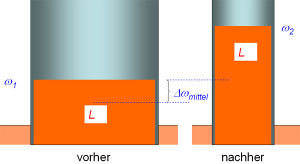
Alle möglichen Zusammenhänge der Rotationsmechanik können im Flüssigkeitsbild dargestellt werden. Dabei gilt folgende Zuordnung

Drehimpuls = "schwere" Flüssigkeit
Winkelgeschwindigkeit = Füllhöhe
Trägheitsmoment = Grundfläche der Töpfe
zugeordneter Energiestrom = potentielle Energie des Flüssigkeitsstromes
Prozessleistung = Prozessleistung des Flüssigkeitsstromes
Rotationsenergie = Inhalt mal halbe Füllhöhe
freigesetzte Energie = geflossene Menge mal mittlere Fallhöhe

Die Drehimpulsbilanz wird so zu einer Volumenbilanz und die Rotationsenergie ist als potentielle Energie der Flüssigkeit zu erkennen.

Sogar die Dynamik der Pirouette lässt sich im Flüssigkeitsbild leicht analysieren. Verkleinert die Eiskunstläuferin ihr Trägheitsmoment, erscheint dieser Vorgang im Flüssigkeitsbild als ein Hochquetschen des gespeicherten Drehimpulses. Die von der Läuferin aufzuwendende Energie ist damit gleich der gespeicherten Flüssigkeit mal Höhenänderung des zugehörigen "Schwerpunktes", also gleich Drehimpuls mal halbe Änderung der Winkelgeschwindigkeit.

Analogie

Die Translationsmechanik längs einer Geraden und die Rotationsmechanik um eine Achse weisen viele Analogien auf. Zur Optimierung des Lernprozesses sollten Sie diese Symmetrie ausnutzen.

Element	Translation	Einheit	Rotation	Einheit
Menge	Impuls	Ns	Drehimpuls	Nms
Potenzial	Geschwindigkeit	m/s	Winkelgeschwindigkeit	1/s
Stromstärke	Kraft	N	Drehmoment	Nm
Energiestrom	[math]P(F)=F_xv_x[/math]	W	[math]P(M)=M_x\omega_x[/math]	W
Kapazität	Masse	[m] = kg	Trägheitsmoment	[J] = kgm²
Widerstand	[math]F=k\Delta v[/math]	[k]=Ns/m	[math]M=k\Delta \omega[/math]	[k]=Nms
Induktivität	[math]F=D\Delta s[/math]	[D] = N/m	[math]M=D\Delta \varphi[/math]	[D] = Nm
kapazitive Energie	kinetische Energie: [math]W=\frac{m}{2}v^2[/math]	[W_kin] = J	Rotationsenergie: [math]W=\frac{J}{2}\omega^2[/math]	[W_rot] = J

Kontrollfragen

In welchen Einheiten misst man den Drehimpuls und das Trägheitsmoment?
Wie fliesst der Drehimpuls durch den Osprey hindurch?
Wo fliesst die Energie im Osprey mit und wo gegen den Drehimpulsstrom?
Eine Antriebswelle dreht sich 5000 Mal in der Sekunde. Wie stark ist der durchfliessende Drehimpulsstrom (Drehmoment auf eine Schnittfläche), falls 25 kW Leistung (zugeordneter Energiestrom) übertragen wird?
Eine Eiskunstläuferin dreht sich nach dem Einziehen von Arme und Beine drei Mal schneller als vorher. Um wie viel Prozent hat die Rotationsenergie zugenommen?
Welche Grössen der Rotationsmechanik sind analog zu Impuls, Geschwindigkeit, Masse, Kraft und kinetische Energie?

Antworten zu den Kontrollfragen

Das Trägheitsmoment wird in Kilogramm mal Quadratmeter gemessen. Dem Drehimpuls ist somit die Einheit Kilogramm mal Quadratmeter durch Sekunde zuzuordnen. Dies entspricht der Einheit Newton mal Meter mal Sekunde.
Der Osprey entzieht der Luft mit einem Propeller dauernd Drehimpuls und leitet ihn unverzüglich an den andern Propeller weiter, der ihn an die Luft weg pumpt.
Im einen Antriebssystem fliesst die Energie vom Motor gegen den Drehimpulsstrom an den Propeller und von dort an die Luft weg. Im zweiten Antriebssystem fliesst die Energie zusammen mit dem Drehimpuls vom Motor zum Propeller und von dort an die Luft weg.
In der Antriebswelle fliesst ein Drehimpulsstrom der Stärke I_L = 25'000 W : (2*π*5000) = 0.8 Nm. Die Stärke eines Drehimpulsstromes bezüglich einer Schnittfläche nennt man auch Drehmoment.
Vernachlässigt man den Drehimpulsaustausch zwischen der Läuferin und dem Eis, nimmt die Rotationsenergie beim Verdreifachen der Drehzahl ebenfalls um Faktor drei zu. Dies entspricht einem Zuwachs von 200%.
Folgende Grössen sind paarweise analog: Impuls / Drehimpuls; Geschwindigkeit / Winkelgeschwindigkeit; Masse / Trägheitsmoment; Kraft / Drehmoment; kinetische Energie / Rotationsenergie.

Materialien

Physik und Systemwissenschaft in Aviatik 2014

Physik und Systemwissenschaft in Aviatik