Schwenkbewegung und Unwucht: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (30 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Ein Körper bewegt sich, sobald sein |
Ein Körper bewegt sich, sobald sein [[Impuls]]inhalt ungleich Null ist. Analog dazu verursacht der [[Drehimpuls]] eine Rotation. Die Rotation eines [[starrer Körper|starren Körpers]] unterscheidet sich aber in zwei wesentlichen Punkten von der Translation |
||
#der Zusammenhang zwischen Drehimpuls und Winkelgeschwindigkeit wird durch einen [[Tensor]] vermittelt |
#der Zusammenhang zwischen Drehimpuls und Winkelgeschwindigkeit wird durch einen [[Tensor]] vermittelt |
||
#die Drehungen bilden eine Gruppe und keinen Vektorraum wie die Verschiebungen |
#die Drehungen bilden nur eine Gruppe und somit keinen Vektorraum wie die Verschiebungen |
||
Nachfolgend wird zuerst ein kurzer Überblick über die Mechanik des starren Körpers gegeben. Danach |
Nachfolgend wird zuerst ein kurzer Überblick über die Mechanik des starren Körpers gegeben. Danach wenden wir uns der Schwenkbewegung eines Rotors zu. Im letzten Teil werden statische und dynamische [[Unwucht]] erklärt. |
||
==Lernziele== |
==Lernziele== |
||
In dieser Vorlesung lernen Sie |
In dieser Vorlesung lernen Sie |
||
*wie die Mechanik des [[starrer Körper|starren Körpers]] strukturiert ist |
|||
*worin sich die [[Rotationsmechanik|Mechanik der Rotation]] von der [[Translationsmechanik|Mechanik der Translation]] unterscheidet |
|||
*wie die [[Energiebilanz]] bezüglich eines starren Körpers formuliert wird |
|||
*was man unter der [[Hauptachse]] eines starren Körpers versteht |
|||
*was eine [[Nutation]] ist |
|||
*wie das Drehmoment bei der Schwenkbewegung eines Kreisels mit der zugehörigen [[Winkelgeschwindigkeit]] und dem [[Drehimpuls]] zusammenhängt |
|||
*wie die Präzessionsbewegung zustande kommt |
|||
*was der Unterschied zwischen statischer und dynamischer [[Unwucht]] ist |
|||
*wie man die Belastung der Lager bei einer Unwucht berechnet |
|||
==starrer Körper== |
==starrer Körper== |
||
| Zeile 11: | Zeile 20: | ||
===Grundgesetze=== |
===Grundgesetze=== |
||
Ein starrer speichert [[Impuls]] und [[Drehimpuls]], wobei die Summe über die zugehörigen Strom- und Quellenstärken die Änderungsraten des Inhalts festlegt. Die Stärken der Impulsströme bezüglich eines ausgewählten Körpers nennt man Oberflächenkräfte, die Gewichtskraft bildet eine Impulsquelle |
Ein starrer Körper speichert [[Impuls]] und [[Drehimpuls]], wobei die Summe über die zugehörigen Strom- und Quellenstärken die Änderungsraten des Inhalts festlegt. Die Stärken der Impulsströme bezüglich eines ausgewählten Körpers nennt man Oberflächenkräfte, die Gewichtskraft bildet eine Impulsquelle |
||
:<math> \sum_i\vec F_i+m\vec g=\dot{\vec p}</math> |
:<math> \sum_i\vec F_i+m\vec g=\dot{\vec p}</math> |
||
Im Gegensatz zum Impuls ist der Drehimpuls nicht lokalisierbar, d.h. es gibt weder Dichten noch Stromdichten. Dennoch kann man bezüglich ganzer Bauteile eine zur Impulsbilanz analoge |
Im Gegensatz zum Impuls ist der Drehimpuls nicht lokalisierbar, d.h. es gibt weder Dichten noch Stromdichten. Dennoch kann man bezüglich ganzer Bauteile eine zur Impulsbilanz analoge Drehimpulsbilanz formulieren |
||
:<math> \sum_i\vec M_i+\sum_j(\vec r_j\times\vec F_j)=\dot{\vec L}</math> |
:<math> \sum_i\vec M_i+\sum_j(\vec r_j\times\vec F_j)=\dot{\vec L}</math> |
||
Reine Drehmomente entstehen durch die Einwirkung des [[elektromagnetisches Feld|elektromagnetischen Feldes]], verdrehte Wellen oder gebogene Balken. Solche |
Reine Drehmomente (erster Term) entstehen durch die Einwirkung des [[elektromagnetisches Feld|elektromagnetischen Feldes]], durch verdrehte Wellen oder gebogene Balken. Solche Drehmomente lassen sich ersatzweise als [[Kräftepaar]]e darstellen. Weitere Drehmomente (zweiter Term) treten in Begleitung von Kräften auf. Sobald die [[Wirklinie]] einer Kraft nicht durch den Massenmittelpunkt des Körpers geht, muss der Kraft ein Drehmoment '''zugeordnet''' werden ([[Hebelgesetz]]). Der Betrag des zugeordneten Drehmoments ist gleich Kraft mal Abstand des Massenmittelpunktes von der Wirklinie der Kraft. Die Richtung des Drehmoments steht normal zu der Ebene, die von der Wirklinie und dem Massenmittelpunkt aufgespannt wird. Die Zuordnung eines Drehmoments zu einem Kräftepaar bzw. zu einer Kraft und dem Massenmittelpunkt beruht auf dem Umstand, dass ein seitwärts fliessender Impulsstrom immer eine Drehimpulsquelle oder -senke induziert. Das einer Kraft zugeordneten Drehmoment verhält sich analog zur Leistung dieser Kraft ([[zugeordneter Energiestrom]]) |
||
*die Leistung einer Kraft wird zur [[Prozessleistung]], sobald der zugehörige Impulsstrom eine Geschwindigkeitsdifferenz "durchfällt" |
*die Leistung einer Kraft wird zur [[Prozessleistung]], sobald der zugehörige Impulsstrom eine Geschwindigkeitsdifferenz "durchfällt" |
||
*das einer Kraft zugeordnete Drehmoment wird zu einer Drehimpulsquelle, sobald der zugehörige Impulsstrom quer zur Bezugsrichtung fliesst |
*das einer Kraft zugeordnete Drehmoment wird zu einer Drehimpulsquelle, sobald der zugehörige Impulsstrom quer zur Bezugsrichtung fliesst |
||
Zu der [[Impulsbilanz]] gesellt sich das [[kapazitives Gesetz|kapazitive Gesetz]]: der Impulsinhalt legt die Geschwindigkeit des Massenmittelpunkts fest |
|||
:<math>\vec v_{MMP}=\frac{\vec p}{m}</math> |
:<math>\vec v_{MMP}=\frac{\vec p}{m}</math> |
||
| Zeile 46: | Zeile 55: | ||
===Energie=== |
===Energie=== |
||
Die Energiebilanz |
Die Energiebilanz bezüglich des starren Körpers kann direkt aus der Impuls- und der Drehimpulsbilanz abgeleitet werden. Man erhält dann folgende Vorschriften |
||
#jeder Kraft ist eine Leistung zuzuordnen <math>P(\vec F)=\vec F\cdot\vec v_A</math>, wobei immer die Geschwindigkeit des Kraftangriffspunktes ''A'' genommen werden muss |
#jeder Kraft ist eine Leistung zuzuordnen <math>P(\vec F)=\vec F\cdot\vec v_A</math>, wobei immer die Geschwindigkeit des Kraftangriffspunktes (''A'') genommen werden muss |
||
#jedem nicht einer Kraft zugeordneten Drehmoment ist ebenfalls eine Leistung zuzuweisen <math>P(\vec M)=\vec M\cdot\vec\omega</math> |
#jedem nicht einer Kraft zugeordneten Drehmoment ist ebenfalls eine Leistung zuzuweisen <math>P(\vec M)=\vec M\cdot\vec\omega</math> |
||
#die Bewegungsenergie spaltet sich in eine [[kinetische Energie]] |
#die Bewegungsenergie spaltet sich in eine [[kinetische Energie]] und eine [[Rotationsenergie]] |
||
::<math>W_{kin}=\vec p\cdot\frac{\vec v_{MMP}}{2}=\frac m2\left(v_x^2+v_y^2+v_z^2\right)</math> |
|||
::<math>W_{rot}=\vec L\cdot\frac{\vec\omega}{2}</math> |
|||
Nach diesen Klarstellungen kann die Energiebilanz bezüglich eines starren Körpers formuliert werden |
Nach diesen Klarstellungen kann die Energiebilanz bezüglich eines starren Körpers formuliert werden |
||
:<math>\sum_i P(\vec F_i)+\sum_j P(\vec M_j)=\dot W_{kin}+\dot W_{rot}</math> |
:<math>\sum_i P(\vec F_i)+\sum_j P(\vec M_j)=\dot W_{kin}+\dot W_{rot}</math> |
||
Die Energiebilanz bringt |
Die Energiebilanz bringt hier keine zusätzlichen Informationen. Dennoch ist sie für das Verständnis hilfreich. Werden mehrere starre Körper über Gelenke miteinander verbunden oder wird der Körper durch eine Führung (Schiene, starre Achse) auf eine bestimmte Bahn gezwungen, lassen sich viele Probleme mit Hilfe der Energie effizient formulieren und lösen. |
||
===Hauptachsen=== |
===Hauptachsen=== |
||
Jeder starre Körper besitzt mindestens drei zueinander normal stehende Achsen, bezüglich denen die Winkelgeschwindigkeit |
Jeder starre Körper besitzt mindestens drei zueinander normal stehende Achsen ('''Hauptachsen'''), bezüglich denen die [[Winkelgeschwindigkeit]] und der [[Drehimpuls]] in die gleiche Richtung zeigen |
||
:<math>L=J_i\omega</math> mit ''i'' =1, 2, 3 |
:<math>L=J_i\omega</math> mit ''i'' =1, 2, 3 |
||
Die Hauptachsen-Trägheitsmomente werden oft der Grösse nach nummeriert <math>J_1 < J_2 < J_3</math>. So verläuft bei einem Ziegelstein die erste Achse parallel zur längsten und die dritte Achse parallel zur kürzesten Kante. Schreibt man die kinetische Energie in Funktion des Drehimpulses, wird ein zur [[Pirouette]] analoger Zusammenhang erkennbar |
|||
:<math>W_{rot}=\frac{L^2}{2J_3}<\frac{L^2}{2J_2}<\frac{L^2}{2J_1}</math> |
:<math>W_{rot}=\frac{L^2}{2J_3}<\frac{L^2}{2J_2}<\frac{L^2}{2J_1}</math> |
||
Je grösser das Massenträgheitsmoment, desto geringer die [[Energie]] bei gegebenem [[Drehimpuls]]. |
|||
| ⚫ | Sind die Lage der Hauptachsen im Körper und die Grössen der drei zugehörigen Trägheitsmomente bekannt, lassen sich die neun Komponenten des |
||
| ⚫ | Sind die Lage der Hauptachsen im Körper und die Grössen der drei zugehörigen Trägheitsmomente bekannt, lassen sich die neun Komponenten des Trägheits-Tensors für eine beliebige Ausrichtung mittels einer Transformation bestimmen. Dazu führt man ein körperfestes Koordinatensystem ein, dessen Achsen nach den Hauptachsen ausgerichtet sind. Die Rotationsmatrix ''R(t)'', die aus der Winkelgeschwindigkeit zu berechnen ist, transformiert das Weltsystem in das körpereigene System. Für das Massenträgheitsmoment gilt dann |
||
:<math>\boldsymbol J(t)=R(t)\boldsymbol J_0 R^T(t)</math> |
:<math>\boldsymbol J(t)=R(t)\boldsymbol J_0 R^T(t)</math> |
||
| Zeile 71: | Zeile 84: | ||
===Nutation=== |
===Nutation=== |
||
Rotiert ein Körper um die Achse mit dem grössten Massenträgheitsmoment, ist seine Rotationsenergie bei gegebenen [[Drehimpuls]] minimal. Bei einer Rotation um die Achse mit dem kleinsten Trägheitsmoment wird die Energie maximal. Lässt man nun einen im Schwerpunkt drehbar gelagerten Körper frei |
Rotiert ein Körper um die Achse mit dem grössten Massenträgheitsmoment, ist seine Rotationsenergie bei gegebenen [[Drehimpuls]] minimal. Bei einer Rotation um die Achse mit dem kleinsten Trägheitsmoment wird die Energie maximal. Lässt man nun einen im Schwerpunkt drehbar gelagerten Körper frei rotieren (ohne Einwirkung von Kräften und Drehmomenten), ist die Rotation um die Hauptachsen mit dem kleinsten und grössten Trägheitsmoment stabil, weil es nur je eine Winkelgeschwindigkeit gibt, bei welcher Drehimpuls und Energie den gegebenen Wert annehmen können. Versetzt man den Körper um eine andere Achse in Rotation, überstreicht die Drehachse bei konstantem Drehimpuls und fester Rotationsenergie einen Kegel. Das Herumwirbeln der Drehachse bei konstantem Drehimpuls nennt man Nutation. Eine Nutation setzt auch ein, falls man die Rotation bei der mittleren Hauptachse beginnt. Die Rotation um die mittlere Hauptachse ist demnach instabil. |
||
Die Erkenntnis, dass ein starrer Körper um mindestens zwei Achsen (bei Symmetrien können es mehr sein) stabil rotieren kann, geht auf ''Leonhard Euler'' zurück und ist somit mindestens 200 Jahre alt. Deshalb waren die Ingenieure bei der NASA äusserst erstaunt, als ihr erster Satellit, [http://en.wikipedia.org/wiki/Explorer_1 Explorer 1], schon nach kurzer Zeit ins Trudeln kam und schlussendlich quer zur Symmetrieachse rotierte. Nach dem Start |
Die Erkenntnis, dass ein starrer Körper um mindestens zwei Achsen (bei Symmetrien können es mehr sein) stabil rotieren kann, geht auf ''Leonhard Euler'' zurück und ist somit mindestens 200 Jahre alt. Deshalb waren die Ingenieure bei der NASA äusserst erstaunt, als ihr erster Satellit, [http://en.wikipedia.org/wiki/Explorer_1 Explorer 1], schon nach kurzer Zeit ins Trudeln kam und schlussendlich quer zur Symmetrieachse rotierte. Nach dem Start wurde der Satellit um seine Längsachse, also um die Achse mit dem kleinsten Massenträgheitsmoment in Rotation versetzt. In diesem Zustand ist die Rotationsenergie bei gegebenem Drehimpuls maximal. Weil die flexiblen Antennen danach durch Schwingungen Energie [[Dissipation|dissipierten]], ging der Satellit in den Zustand kleinster Rotationsenergie über. Und das ist bei gegebenem Drehimpuls eine Achse mit dem maximalen Massenträgheitsmoment, also eine Achse quer zur Längsrichtung des Satelliten. |
||
==konstante Bewegungsenergie== |
==konstante Bewegungsenergie== |
||
Wirkt eine Kraft normal zur Geschwindigkeit auf einen Körper ein, ändert sich sein [[Impuls]], nicht aber seine [[Energie]]. Es findet keine Energieaustausch statt, weil die [[Leistung einer Kraft|Leistung der Kraft]] gleich Null ist. Analog verhält es sich mit einem normal zur Winkelgeschwindigkeit stehenden Drehmoments. |
|||
===Kreisbewegung=== |
===Kreisbewegung=== |
||
Eine [[gleichmässige Kreisbewegung]] erfordert eine Kraft, die normal zur Geschwindigkeit steht und gegen das Kreiszentrum zeigt. Der Betrag diese Normalkraft, die auch [[Zentripetalkraft]] heisst, ist proportional zum Produkt aus dem Betrag von Impuls und Winkelgeschwindigkeit |
[[Bild:Kreisbewegung KraftundImpuls.png|thumb|Kraft, Impuls und Winkelgeschwindigkeit]]Eine [[gleichmässige Kreisbewegung]] erfordert eine Kraft, die normal zur Geschwindigkeit steht und gegen das Kreiszentrum zeigt. Der Betrag diese Normalkraft, die auch [[Zentripetalkraft]] heisst, ist proportional zum Produkt aus dem Betrag von Impuls und Winkelgeschwindigkeit |
||
:<math>F_N=m\frac{v^2}{r}=p\frac vr=p\omega</math> |
:<math>F_N=m\frac{v^2}{r}=p\frac vr=p\omega</math> |
||
| Zeile 85: | Zeile 98: | ||
Diese rein dynamische Formulierung lässt sich nun auch vektoriell schreiben |
Diese rein dynamische Formulierung lässt sich nun auch vektoriell schreiben |
||
:<math>\vec |
:<math>\vec F_N=\vec \omega\times\vec p=\frac{d\vec p}{dt}</math> |
||
Ändert der Impuls nur seine Richtung, nicht aber seinen Betrag, steht die Änderungsrate und somit die resultierende Kraft normal zum Impuls. In der Physik kennt zwei Kräfte, die |
Ändert der Impuls nur seine Richtung, nicht aber seinen Betrag, steht die Änderungsrate und somit die resultierende Kraft normal zum Impuls. In der Physik kennt man zwei Kräfte, die andauernd normal zur Geschwindigkeit des Körpers stehen und folglich mit dem Körper Impuls, aber keine Energie austauschen |
||
:[[Corioliskraft]] auf einen bewegten Körper im rotierenden Bezugssystem: <math>\vec F_C=2m(\vec v\times\vec\omega_{System})</math> |
:[[Corioliskraft]] auf einen bewegten Körper im [[rotierendes Bezugssystem|rotierenden Bezugssystem]]: <math>\vec F_C=2m(\vec v\times\vec\omega_{System})</math> |
||
:[[Lorentzkraft]] auf eine bewegte Ladung im Magnetfeld: <math>\vec F_B=Q(\vec v\times\vec B)</math> |
:[[Lorentzkraft]] auf eine bewegte Ladung im Magnetfeld: <math>\vec F_B=Q(\vec v\times\vec B)</math> |
||
| Zeile 96: | Zeile 109: | ||
===Schwenkbewegung=== |
===Schwenkbewegung=== |
||
Steht das einwirkende Drehmoment normal |
[[Bild:Schwenken.png|thumb|Kreisel schwenkt im Gegenuhrzeigersinn]]Steht das einwirkende Drehmoment normal zur [[Winkelgeschwindigkeit]], ist die Leistung des Drehmoments gleich Null und der Körper ändert seine Rotationsenergie nicht. So kann jedes schwenkbar gelagerte Rad seinen [[Drehimpuls]] bei konstant gehaltener [[Rotationsenergie]] ändern. Dazu muss die Achse des rotierenden Rads gedreht werden. Formal gilt ein zur [[Kreisbewegung]] analoger Zusammenhang |
||
:<math>\vec M=\vec\omega_S\times\vec L=\frac{d\vec L}{dt}</math> |
:<math>\vec M=\vec\omega_S\times\vec L=\frac{d\vec L}{dt}</math> |
||
Mit ''ω<sub>S</sub>'' ist die Winkelgeschwindigkeit der Schwenkbewegung und nicht die Winkelgeschwindigkeit des sich drehenden Rades gemeint. |
Mit ''ω<sub>S</sub>'' ist die Winkelgeschwindigkeit der Schwenkbewegung und nicht etwa die Winkelgeschwindigkeit des sich drehenden Rades gemeint. Die Formel verknüpft drei Grössen, wobei zwei, das Drehmoment und die Winkelgeschwindigkeit der Schwenkbewegung, wahlweise als ursächlich angesehen werden können. Eine Schwierigkeit bei der Anwendung dieser Formel ist die [[rechte Hand Regel|Regel der rechten Hand]], die bei allen drei Grössen und beim Vektorprodukt angewendet werden muss |
||
*Drehimpuls: Finger der rechten Hand um das Rad in Rotationsrichtung legen; Daumen zeigt die Richtung des Drehimpulses an |
*Drehimpuls: Finger der rechten Hand um das Rad in Rotationsrichtung legen; Daumen zeigt die Richtung des Drehimpulses an |
||
*Schwenkbewegung: Finger der rechten Hand in die Ebene legen, in welche die Achse des Rades gekippt wird; Daumen zeigt in Richtung der Winkelgeschwindigkeit der Schwenkbewegung |
*Winkelgeschwindigkeit der Schwenkbewegung: Finger der rechten Hand in die Ebene legen, in welche die Achse des Rades gekippt wird; Daumen zeigt in Richtung der Winkelgeschwindigkeit der Schwenkbewegung |
||
*Drehmoment: Finger der rechten Hand in Wirkrichtung des Drehmoments legen; Daumen zeigt in Richtung des Drehmoments (Schraube anziehen) |
*Drehmoment: Finger der rechten Hand in Wirkrichtung des Drehmoments legen; Daumen zeigt in Richtung des Drehmoments (Schraube anziehen) |
||
*Vektorprodukt: Daumen |
*Vektorprodukt: Daumen parallel zur Winkelgeschwindigkeit der Schwenkbewegung legen; Zeigefinger nach dem Drehimpuls ausrichten; Mittelfinger zeigt in Richtung des Drehmoments. |
||
Trägt man alle drei Vektoren (Drehimpuls, Winkelgeschwindigkeit der Schwenkbewegung, Drehmoment) in eine Skizze ein, ist die Anwendung des Vektorprodukts keine grosse Hexerei. |
|||
'''Beispiel Motorrad:''' Die Frage eines [http://r6club.de/ Yamaha-Fahrers] zeigt die Problematik der Kurvenfahrt mit einem |
'''Beispiel Motorrad:''' Die Frage eines [http://r6club.de/ Yamaha-Fahrers] zeigt die Problematik der Kurvenfahrt mit einem Motorrad: "Wenn ich eine Linkskurve einleiten will, drücke ich den Lenker auf der linken Seite nach vorne. Das Vorderrad zeigt also von der Zentrallinie abweichend nach rechts. Dadurch verschiebt sich der Schwerpunkt nach links und das Motorrad fährt eine Linkskurve. Wenn ich jetzt aber besonders langsam fahre (zum Beispiel bei der Fahrübung, wo man eine 8 fahren muss - kennen sicher noch einige von der praktischen Prüfung), dann funktioniert das Ganze umgekehrt. Sprich wenn ich nach links fahren möchte ist der Lenker auch ganz nach links eingeschlagen. Wie funktioniert es also eigentlich, dass das Motorrad eine Kurve fahren kann?" |
||
Wäre die Erklärung mit dem Schwerpunkt richtig, müsst sie auch beim Skibob oder Snowbike funktionieren. Mit diesen Geräten fährt man auch mit hoher |
Wäre die Erklärung mit dem Schwerpunkt richtig, müsst sie auch beim Skibob oder Snowbike funktionieren. Mit diesen Geräten fährt man auch mit hoher Geschwindigkeit in eine Kurve. Der entscheidende Effekt kommt aber vom Drehimpuls des Vorderrades. Drückt man den Lenker links nach vorn, wirkt ein nach unten gerichtetes Drehmoment auf das Vorderrad ein. Weil der Drehimpuls nach links zeigt, kippt das Rad nach links und der Töff neigt sich auf die richtige Seite. Zur Überprüfung dieses Zusammenhangs lege man den Daumen parallel zur Winkelgeschwindigkeit der Schwenkbewegung, also nach hinten. Der Zeigfinger, welcher in Richtung des Drehimpulses anzeigt, weist nach links. Daraus ergibt sich ein nach unten gerichtetes Drehmoment. Und dieses Moment erzeugt der Fahrer, indem er den Lenker mit der linken Hand nach vorne drückt. |
||
'''Beispiel Wendezeiger:''' Der [[Wendezeiger]] (Turn Indicator) ist ein Kreiselinstrument, das die Winkelgeschwindigkeit des |
'''Beispiel Wendezeiger:''' Der [[Wendezeiger]] (Turn Indicator) ist ein Kreiselinstrument, das die Winkelgeschwindigkeit des Flugzeuges um die Hochachse anzeigt. Der halb[[kardanisch]] gelagerte Kreisel rotiert parallel zur Querachse des Flugzeuges. Nun kann der Käfig, der den Kreisel lagert, um eine parallel zum Flugzeug gerichtete Achse gedreht werden. Diese Drehung ist mit einer Rückstellfeder gekoppelt. Weist der Drehimpulsvektor des Kreisels vom Pilot aus gesehen nach rechts und dreht sich das Flugzeug um die Hochachse nach links, muss ein nach vorne weisendes Drehmoment auf den Kreisel einwirken, damit dieser die Drehbewegung des Flugzeuges mitmacht. Dazu kippt die Kreiselachse leicht nach links, bis die Feder stark genug gespannt ist. Die Stärke der Kippbewegung zeigt so die Grösse der Winkelgeschwindigkeit an. |
||
'''Beispiel |
'''Beispiel Strahltriebwerk:''' Fan, Kompressor und Turbine eines Strahltriebwerkes rotieren mit hoher Drehzahl und speichern entsprechend viel Drehimpuls. Fliegt nun ein Flugzeug eine Kurve, muss ein grosses Drehmoment auf das Triebwerk einwirken, damit sich dieses mit dem Flugzeug dreht. Das Drehmoment steht normal zum Triebwerk und liegt in der Kurvenebene drin. Eine schnelle Rotation um die Querachse (unsanfte Landung oder Looping) belastet die Aufhängung der Triebwerke eher noch stärker als der Kurvenflug. |
||
===Präzession=== |
===Präzession=== |
||
Wirkt auf einen Kreisel über längere Zeit ein [[Drehmoment]] ein, das normal zum Drehimpuls gerichtet ist, setzt gemäss der weiter oben aufgeführten Formel eine Schwenkbewegung ein. Die Kreiselachse überstreicht dann den Mantel eines Kegels. Diese Bewegung nennt man Präzession. |
[[Bild:Präzession.png|thumb|Präzession]]Wirkt auf einen Kreisel über längere Zeit ein [[Drehmoment]] ein, das normal zum Drehimpuls gerichtet ist, setzt gemäss der weiter oben aufgeführten Formel eine Schwenkbewegung ein. Die Kreiselachse überstreicht dann den Mantel eines Kegels. Diese Bewegung nennt man Präzession. Im Demonstrationsexperiment zur Präzession (die Skizze zeigt ein etwas anderes Experiment) belastet man einen [[kardanische Aufhängung|kardanisch]] aufgehängten, horizontal rotierenden Kreisel mit einem seitlich angebrachten Zusatzkörper. Die Gewichtskraft dieses Zusatzkörpers erzeugt dann über die [[Hebelgesetz|Hebelwirkung]] ein Drehmoment ''M'' auf den Kreisel. Weil dieses Drehmoment die Schwenkbewegung mitmacht, stellt sich eine stationäre Präzessionsbewegung ein. Die Präzessionsperiode ist gleich |
||
:<math>T_P=\frac{2\pi}{\omega_S}=\frac{2\pi L}{M}</math> |
:<math>T_P=\frac{2\pi}{\omega_S}=\frac{2\pi L}{M}</math> |
||
Im Demonstrationsversuch hängt man den Zusatzkörper an die anfangs ruhende Achse. Der Kreisel kippt dann zuerst nach unten, um dann in eine Präzessionsbewegung überzugehen, die von einer gedämpften Nutation überlagert wird. Mit der Kippbewegung stellt der Kreisel Drehimpuls für die Präzessionsbewegung zur Verfügung. Würde keine Reibung auftreten, käme der Kreisel nach jeder Nutationsperiode in horizontaler Lage wieder zur Ruhe. Um die Nutation zu verhindern, stösst man beim Aufhängen des Zusatzkörpers den Kreisel so weg, dass er von Anfang an den für die Präzession notwendigen Drehimpuls besitzt. Dann dreht sich der Kreisel anfänglich horizontal. Infolge der Reibung wird er sich dennoch immer stärker vertikal ausrichten. |
|||
'''Beispiel Präzession der Erde:''' Mond und Sonne wirken mit je einem periodisch anschwellenden Drehmoment auf die Erde ein und versuchen |
'''Beispiel Präzession der Erde:''' Mond und Sonne wirken mit je einem periodisch anschwellenden Drehmoment auf die Erde ein und versuchen sie aufzurichten. Ursache dieser Einwirkung ist "Äquatorwulst", die rotationsbedingte Abplattung der Erde. Auf diese Einwirkung reagiert die Erde mit einer lunisolaren Präzession. Die Erdachse benötigt für einen einzigen Umlauf auf dem Präzessionskegel zwischen 25.700 und 25.800 Jahre. Dieser Zeitraum wird auch platonisches Jahr genannt. Weil unser Kalender an den Frühlingspunkt (Äquinoktium) gebunden ist, verschieben sich die Monate infolge der Präzession etwa alle 2000 Jahre um ein Sternzeichen. |
||
==Unwucht== |
==Unwucht== |
||
Rotierende Maschinenelemente wie Räder, [[Propeller]] oder Turbinen müssen ausgewuchtet sein, damit die Lager nicht unnötig belastet werden. Man unterscheidet zwischen statischer und dynamischer [[Unwucht]]. Bei der statischen Unwucht ändert sich der [[Impuls]] und bei der dynamischen der [[Drehimpuls]] bei konstant gehaltener [[Bewegungsenergie]]. Zur Erklärung dieses Phänomens gehen wir von einer ausgewuchteten Scheibe aus, die entlang des Umfangs mehrere, achsenparallele Gewindelöcher aufweist. In diese Bohrungen können kurze Schrauben eingedreht werden, um so gezielt eine Unwucht zu erzeugen. |
|||
===statische Unwucht=== |
===statische Unwucht=== |
||
[[Bild:Unwucht Scheibe.png|thumb|statische und dynamische Unwucht]]Dreht man zwei kurze Schrauben (Masse m<sub>S</sub>) von beiden Seiten in das gleiche Gewindeloch, verschiebt sich der Massenmittelpunkt des Gesamtsystems weg von der Scheibenachse. Der Impulsinhalt von rotierender Scheibe und Schrauben ist gleich gross wie der eines punktförmigen Körpers gleicher Masse, der sich im Abstand ''r<sub>MMP</sub>'' auf einer Kreisbahn um die Achse bewegt |
|||
:<math>p=2m_Sv_S=2m_Sr_S\omega=mr_{MMP}\omega</math> |
|||
Damit sich der Impulsinhalt synchron mit der Drehung ändert, muss von den Lagern eine Kraft einwirken |
|||
:<math>F_L=\omega p=mr_{MMP}\omega^2</math> |
|||
Die Lagerkraft steigt quadratisch mit der Drehzahl. Deshalb müssen schnell drehende Körper speziell gut ausgewuchtet sein. |
|||
===dynamische Unwucht=== |
===dynamische Unwucht=== |
||
[[Bild:Unwucht2.jpg|thumb|statische und dynamische Unwucht]]Befestigt man die Schrauben so in zwei gegenüber liegenden Löchern, dass ihre Köpfe auf je einer Seite der Scheibe heraus ragen, entsteht eine dynamische Unwucht. Obwohl der Massenmittelpunkt des Gesamtsystems weiterhin auf der Drehachse liegt, werden die Lager mit zunehmender Drehzahl belastet. Zur Analyse bilden wir den [[Bahndrehimpuls]] der beiden Schrauben. Dieser Bahndrehimpuls steht leicht schief zur Scheibenachse und bewegt sich auf einem Kreiskegel. Nun bleibt die zur Drehachse (Winkelgeschwindigkeit) parallele Komponente des Drehimpulses erhalten. Die Radialkomponente wird dagegen durch die Drehbewegung herum gewirbelt, macht also eine andauernde Schwenkbewegung. Das zugehörige Drehmoment, das von den Lagern aufgebracht werden muss, ist gleich |
|||
:<math>M_L=\omega L_n=2m_S r_S z_S\omega^2</math> |
|||
wobei ''z<sub>S</sub>'' den Abstand der Massenmittelpunkte der Schrauben von der Symmetrieebene der Scheibe misst. Nun kann man jedem drehbar gelagerten Körper bezüglich der gegebenen Achse ein Deviations- oder Zentrifugalmoment ''J<sub>D</sub>'' zuschreiben, das den Zusammenhang zwischen Radialkomponente des Drehimpulses und Winkelgeschwindigkeit beschreibt |
|||
:<math>L_n=J_D\omega</math> |
|||
Das Drehmoment, das von den Lagern auf den Körper einwirken muss, um dessen Drehachse zu stabilisieren, ist dann gleich |
|||
:<math>M_L=J_D\omega^2</math> |
|||
Hält man die Achse eines rotierenden Körpers mit Hilfe von zwei Lagern stabil und misst je eine Komponente der Lagerkräfte, erhält man zwei zeitabhängige Signale. Aus diesen Lagerkräften können die resultierende Kraft und das resultierende Drehmoment berechnet werden. Beide Grössen nehmen quadratisch mit der Drehzahl zu. Die resultierende Kraft ist zudem proportional zum Abstand des Schwerpunkts von der Drehachse und das Drehmoment nimmt linear mit dem Deviationsmoment zu. |
|||
==Kontrollfragen== |
==Kontrollfragen== |
||
#Formulieren Sie die Impuls- und die Drehimpulsbilanz bezüglich eines starren Körpers mit Ihren eigenen Worten. |
|||
#Worin unterscheidet sich die Drehmechanik von der Translationsmechanik? |
|||
#Formulieren Sie die Energiebilanz bezüglich eines starren Körpers mit Ihren eigenen Worten. |
|||
#Wie muss man einen Ziegelstein hochwerfen, damit er stabil rotiert? |
|||
#Sie halten die beiden Enden der Achse eines rotierenden Rades mit den Händen fest. Überlegen Sie sich, was passiert, wenn man das eine Ende der Achse gegen sich zieht? die Achse einseitig nach oben drückt? Die Antwort können Sie im Versuch herausfinden, aber achten Sie auf Ihre Finger. |
|||
#Wieso verschieben sich die Sternzeichen gegen den Kalender? |
|||
#Wie unterscheiden sich dynamische und statische Unwucht? |
|||
#Wie verändert sich bei einer Unwucht die Belastung der Lager mit steigender Drehzahl? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Die Summe über alle Kräfte (Oberflächenkräfte und Gewichtskraft) verursacht die Änderungsrate des Impulsinhalts. Die Summe über alle Drehmomente (reine und einer Kraft zugeordnete) verursacht die Änderungsrate des Drehimpulsinhalts. |
|||
#In der Drehmechanik ist die Trägheit kein [[Skalar]] wie die [[Masse]] sondern ein [[Tensor]]. Die Drehbewegungen bilden nur eine Gruppe und keinen Vektorraum wie die Verschiebungen. |
|||
#Die Summe über die Leistungen aller Kräfte (Oberflächenkräfte und Gewichtskraft) plus die Summe über die Leistungen aller reinen Drehmomente (ohne die einer Kraft zugeordneten Drehmomente) sind gleich der Änderungsrate der [[kinetische Energie|kinetischen]] und der [[Rotationsenergie]]. |
|||
#Der Ziegelstein muss so geworfen werden, dass er um eine Achse parallel zu kürzesten Kante (grösstes [[Massenträgheitsmoment]]) oder zur längsten Kante (kleinstes Massenträgheitsmoment) rotiert. |
|||
#Ohne Skizze werden Sie kaum auf die richtige Lösung kommen: zeichnen Sie den Vektor des Drehimpulses ein, markieren Sie die Einwirkung, das Drehmoment, mit einem weiteren Pfeil; die Winkelgeschwindigkeit der Schwenkbewegung muss dann die oben formulierte Gesetzmässigkeit erfüllen. |
|||
#Sonne und Mond versuchen die Achse der Erde aufzurichten. Diese reagiert mit einer Präzessionsbewegung. Weil sich der Kalender am Frühlingspunkt (Schnittpunkt der Ekliptik mit dem Äquator) orientiert, wandern die Monate über die Sternzeichen. |
|||
#Bei der statischen Unwucht liegt der [[Massenmittelpunkt]] nicht auf der Drehachse. Deshalb ändert sich der Impulsinhalt periodisch, wodurch die Lager mit einer umlaufenden Kraft belastet werden. Bei der dynamischen Unwucht liegt die Drehachse nicht auf einer Hauptachse des Körpers. Deshalb ändert sich der Drehimpulsinhalt periodisch, wodurch die Lager mit einem umlaufenden Drehmoment belastet werden. |
|||
#Lagerkraft und Lagerdrehmoment nehmen quadratisch mit der Drehzahl zu. |
|||
==Links== |
|||
*[https://cast.switch.ch/vod/clips/ni0ec0pdg/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=LdexQo-xmOg Unwucht] auf Youtube |
|||
*[http://www.youtube.com/watch?v=o1_4Pbb2r5Q Schwenkbewegung] auf Youtube |
|||
*[http://www.youtube.com/watch?v=eGpk9m1VcZE Kurzfassung auf Youtube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik 2014]]''' |
|||
'''[[Physik und Systemwissenschaft in Aviatik |
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
||
[[Kategorie:VorAV]] |
[[Kategorie:VorAV]] |
||
Aktuelle Version vom 21. März 2016, 10:04 Uhr
Ein Körper bewegt sich, sobald sein Impulsinhalt ungleich Null ist. Analog dazu verursacht der Drehimpuls eine Rotation. Die Rotation eines starren Körpers unterscheidet sich aber in zwei wesentlichen Punkten von der Translation
- der Zusammenhang zwischen Drehimpuls und Winkelgeschwindigkeit wird durch einen Tensor vermittelt
- die Drehungen bilden nur eine Gruppe und somit keinen Vektorraum wie die Verschiebungen
Nachfolgend wird zuerst ein kurzer Überblick über die Mechanik des starren Körpers gegeben. Danach wenden wir uns der Schwenkbewegung eines Rotors zu. Im letzten Teil werden statische und dynamische Unwucht erklärt.
Lernziele
In dieser Vorlesung lernen Sie
- wie die Mechanik des starren Körpers strukturiert ist
- worin sich die Mechanik der Rotation von der Mechanik der Translation unterscheidet
- wie die Energiebilanz bezüglich eines starren Körpers formuliert wird
- was man unter der Hauptachse eines starren Körpers versteht
- was eine Nutation ist
- wie das Drehmoment bei der Schwenkbewegung eines Kreisels mit der zugehörigen Winkelgeschwindigkeit und dem Drehimpuls zusammenhängt
- wie die Präzessionsbewegung zustande kommt
- was der Unterschied zwischen statischer und dynamischer Unwucht ist
- wie man die Belastung der Lager bei einer Unwucht berechnet
starrer Körper
Die Mechanik des starren Körpers ist eines der Kernthemen der Ingenieurwissenschaften. Jeder Ingenieur sollte die dieser Mechanik zugrunde liegende Struktur im Prinzip verstehen. Deshalb werden in diesem Abschnitt - aufbauend auf den umfassenden Prinzipien der Physik der dynamischen Systeme - die Gesetze zur Mechanik des starren Körpers nochmals zusammengefasst.
Grundgesetze
Ein starrer Körper speichert Impuls und Drehimpuls, wobei die Summe über die zugehörigen Strom- und Quellenstärken die Änderungsraten des Inhalts festlegt. Die Stärken der Impulsströme bezüglich eines ausgewählten Körpers nennt man Oberflächenkräfte, die Gewichtskraft bildet eine Impulsquelle
- [math] \sum_i\vec F_i+m\vec g=\dot{\vec p}[/math]
Im Gegensatz zum Impuls ist der Drehimpuls nicht lokalisierbar, d.h. es gibt weder Dichten noch Stromdichten. Dennoch kann man bezüglich ganzer Bauteile eine zur Impulsbilanz analoge Drehimpulsbilanz formulieren
- [math] \sum_i\vec M_i+\sum_j(\vec r_j\times\vec F_j)=\dot{\vec L}[/math]
Reine Drehmomente (erster Term) entstehen durch die Einwirkung des elektromagnetischen Feldes, durch verdrehte Wellen oder gebogene Balken. Solche Drehmomente lassen sich ersatzweise als Kräftepaare darstellen. Weitere Drehmomente (zweiter Term) treten in Begleitung von Kräften auf. Sobald die Wirklinie einer Kraft nicht durch den Massenmittelpunkt des Körpers geht, muss der Kraft ein Drehmoment zugeordnet werden (Hebelgesetz). Der Betrag des zugeordneten Drehmoments ist gleich Kraft mal Abstand des Massenmittelpunktes von der Wirklinie der Kraft. Die Richtung des Drehmoments steht normal zu der Ebene, die von der Wirklinie und dem Massenmittelpunkt aufgespannt wird. Die Zuordnung eines Drehmoments zu einem Kräftepaar bzw. zu einer Kraft und dem Massenmittelpunkt beruht auf dem Umstand, dass ein seitwärts fliessender Impulsstrom immer eine Drehimpulsquelle oder -senke induziert. Das einer Kraft zugeordneten Drehmoment verhält sich analog zur Leistung dieser Kraft (zugeordneter Energiestrom)
- die Leistung einer Kraft wird zur Prozessleistung, sobald der zugehörige Impulsstrom eine Geschwindigkeitsdifferenz "durchfällt"
- das einer Kraft zugeordnete Drehmoment wird zu einer Drehimpulsquelle, sobald der zugehörige Impulsstrom quer zur Bezugsrichtung fliesst
Zu der Impulsbilanz gesellt sich das kapazitive Gesetz: der Impulsinhalt legt die Geschwindigkeit des Massenmittelpunkts fest
- [math]\vec v_{MMP}=\frac{\vec p}{m}[/math]
Ein analoger, aber um einiges komplexerer Zusammenhang gilt zwischen Drehimpuls und Winkelgeschwindigkeit
- [math]\vec L=\boldsymbol J\vec\omega[/math] oder [math]\vec \omega=\boldsymbol J^{-1}\vec L[/math]
Das Massenträgheitsmoment J ist ein Tensor, kann also bezüglich des raumfesten Koordinatensystems (Weltsystem) als 3x3-Matrize geschrieben werden.
Die momentane Position des Massenmittelpunktes ergibt sich aus der Geschwindigkeit durch eine Integration über die Zeit
- [math]\vec s_{MMP}(t)=\int_0^t\vec v_{MMP}\tilde dt[/math]
Die Orientierung des Körpers im Raum wird durch die orthonormale Drehmatrix R(t) beschrieben. Diese Matrix transformiert die Komponenten eines Vektors vom Weltsystem in ein körperfestes System. Die Drehmatrix, die drei frei wählbare Parameter besitzt, kann aus der Winkelgeschwindigkeit durch eine Integration über die Zeit ermittelt werden. Um diese Integration auszuführen, benutzt man entweder die Euler-Parametrisierung oder in jüngster Zeit vermehrt die Quaternionen, eine Verallgemeinerung der komplexen Zahlen.
Zusammenfassung: Die drei grundlegenden Schritte zur Formulierung der Mechanik des starren Körpers sind
- Bilanz bezüglich Impuls und Drehimpuls aufstellen
- mit Hilfe der Trägheit (träge Masse, Massenträgheitsmoment) Geschwindigkeit sowie Winkelgeschwindigkeit berechnen
- aus der Geschwindigkeit die Position des Massenmittelpunktes und aus der Winkelgeschwindigkeit die Orientierung im Raum ermitteln.
Sie müssen die einzelnen Schritte nicht bis ins letzte Detail begreifen, sollten aber das ganze Verfahren dem Prinzip nach verstehen.
Energie
Die Energiebilanz bezüglich des starren Körpers kann direkt aus der Impuls- und der Drehimpulsbilanz abgeleitet werden. Man erhält dann folgende Vorschriften
- jeder Kraft ist eine Leistung zuzuordnen [math]P(\vec F)=\vec F\cdot\vec v_A[/math], wobei immer die Geschwindigkeit des Kraftangriffspunktes (A) genommen werden muss
- jedem nicht einer Kraft zugeordneten Drehmoment ist ebenfalls eine Leistung zuzuweisen [math]P(\vec M)=\vec M\cdot\vec\omega[/math]
- die Bewegungsenergie spaltet sich in eine kinetische Energie und eine Rotationsenergie
- [math]W_{kin}=\vec p\cdot\frac{\vec v_{MMP}}{2}=\frac m2\left(v_x^2+v_y^2+v_z^2\right)[/math]
- [math]W_{rot}=\vec L\cdot\frac{\vec\omega}{2}[/math]
Nach diesen Klarstellungen kann die Energiebilanz bezüglich eines starren Körpers formuliert werden
- [math]\sum_i P(\vec F_i)+\sum_j P(\vec M_j)=\dot W_{kin}+\dot W_{rot}[/math]
Die Energiebilanz bringt hier keine zusätzlichen Informationen. Dennoch ist sie für das Verständnis hilfreich. Werden mehrere starre Körper über Gelenke miteinander verbunden oder wird der Körper durch eine Führung (Schiene, starre Achse) auf eine bestimmte Bahn gezwungen, lassen sich viele Probleme mit Hilfe der Energie effizient formulieren und lösen.
Hauptachsen
Jeder starre Körper besitzt mindestens drei zueinander normal stehende Achsen (Hauptachsen), bezüglich denen die Winkelgeschwindigkeit und der Drehimpuls in die gleiche Richtung zeigen
- [math]L=J_i\omega[/math] mit i =1, 2, 3
Die Hauptachsen-Trägheitsmomente werden oft der Grösse nach nummeriert [math]J_1 \lt J_2 \lt J_3[/math]. So verläuft bei einem Ziegelstein die erste Achse parallel zur längsten und die dritte Achse parallel zur kürzesten Kante. Schreibt man die kinetische Energie in Funktion des Drehimpulses, wird ein zur Pirouette analoger Zusammenhang erkennbar
- [math]W_{rot}=\frac{L^2}{2J_3}\lt \frac{L^2}{2J_2}\lt \frac{L^2}{2J_1}[/math]
Je grösser das Massenträgheitsmoment, desto geringer die Energie bei gegebenem Drehimpuls.
Sind die Lage der Hauptachsen im Körper und die Grössen der drei zugehörigen Trägheitsmomente bekannt, lassen sich die neun Komponenten des Trägheits-Tensors für eine beliebige Ausrichtung mittels einer Transformation bestimmen. Dazu führt man ein körperfestes Koordinatensystem ein, dessen Achsen nach den Hauptachsen ausgerichtet sind. Die Rotationsmatrix R(t), die aus der Winkelgeschwindigkeit zu berechnen ist, transformiert das Weltsystem in das körpereigene System. Für das Massenträgheitsmoment gilt dann
- [math]\boldsymbol J(t)=R(t)\boldsymbol J_0 R^T(t)[/math]
Man beachte, dass die inverse Drehmatrix durch Transposition gebildet werden kann. Sobald die aktuelle Darstellung des Massenträgheitsmoments bezüglich des Weltsystems bekannt ist, kann aus dem Drehimpulsinhalt die Winkelgeschwindigkeit gerechnet werden.
Nutation
Rotiert ein Körper um die Achse mit dem grössten Massenträgheitsmoment, ist seine Rotationsenergie bei gegebenen Drehimpuls minimal. Bei einer Rotation um die Achse mit dem kleinsten Trägheitsmoment wird die Energie maximal. Lässt man nun einen im Schwerpunkt drehbar gelagerten Körper frei rotieren (ohne Einwirkung von Kräften und Drehmomenten), ist die Rotation um die Hauptachsen mit dem kleinsten und grössten Trägheitsmoment stabil, weil es nur je eine Winkelgeschwindigkeit gibt, bei welcher Drehimpuls und Energie den gegebenen Wert annehmen können. Versetzt man den Körper um eine andere Achse in Rotation, überstreicht die Drehachse bei konstantem Drehimpuls und fester Rotationsenergie einen Kegel. Das Herumwirbeln der Drehachse bei konstantem Drehimpuls nennt man Nutation. Eine Nutation setzt auch ein, falls man die Rotation bei der mittleren Hauptachse beginnt. Die Rotation um die mittlere Hauptachse ist demnach instabil.
Die Erkenntnis, dass ein starrer Körper um mindestens zwei Achsen (bei Symmetrien können es mehr sein) stabil rotieren kann, geht auf Leonhard Euler zurück und ist somit mindestens 200 Jahre alt. Deshalb waren die Ingenieure bei der NASA äusserst erstaunt, als ihr erster Satellit, Explorer 1, schon nach kurzer Zeit ins Trudeln kam und schlussendlich quer zur Symmetrieachse rotierte. Nach dem Start wurde der Satellit um seine Längsachse, also um die Achse mit dem kleinsten Massenträgheitsmoment in Rotation versetzt. In diesem Zustand ist die Rotationsenergie bei gegebenem Drehimpuls maximal. Weil die flexiblen Antennen danach durch Schwingungen Energie dissipierten, ging der Satellit in den Zustand kleinster Rotationsenergie über. Und das ist bei gegebenem Drehimpuls eine Achse mit dem maximalen Massenträgheitsmoment, also eine Achse quer zur Längsrichtung des Satelliten.
konstante Bewegungsenergie
Wirkt eine Kraft normal zur Geschwindigkeit auf einen Körper ein, ändert sich sein Impuls, nicht aber seine Energie. Es findet keine Energieaustausch statt, weil die Leistung der Kraft gleich Null ist. Analog verhält es sich mit einem normal zur Winkelgeschwindigkeit stehenden Drehmoments.
Kreisbewegung
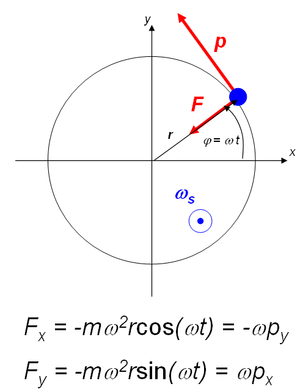
Eine gleichmässige Kreisbewegung erfordert eine Kraft, die normal zur Geschwindigkeit steht und gegen das Kreiszentrum zeigt. Der Betrag diese Normalkraft, die auch Zentripetalkraft heisst, ist proportional zum Produkt aus dem Betrag von Impuls und Winkelgeschwindigkeit
- [math]F_N=m\frac{v^2}{r}=p\frac vr=p\omega[/math]
Diese rein dynamische Formulierung lässt sich nun auch vektoriell schreiben
- [math]\vec F_N=\vec \omega\times\vec p=\frac{d\vec p}{dt}[/math]
Ändert der Impuls nur seine Richtung, nicht aber seinen Betrag, steht die Änderungsrate und somit die resultierende Kraft normal zum Impuls. In der Physik kennt man zwei Kräfte, die andauernd normal zur Geschwindigkeit des Körpers stehen und folglich mit dem Körper Impuls, aber keine Energie austauschen
- Corioliskraft auf einen bewegten Körper im rotierenden Bezugssystem: [math]\vec F_C=2m(\vec v\times\vec\omega_{System})[/math]
- Lorentzkraft auf eine bewegte Ladung im Magnetfeld: [math]\vec F_B=Q(\vec v\times\vec B)[/math]
Die Corioliskraft sorgt dafür, dass sich alle Hochdruckgebiete auf der Nordhalbkugel der Erde im Uhrzeigersinn drehen. Das Magnetfeld der Erde lenkt die geladenen Teilchen (Ionen), die mit grosser Energie von der Sonne auf uns zu fliegen, gegen die Pole ab. Dort erzeugen sie durch Stösse mit den Teilchen der Atmosphäre das Nordlicht.
Schwenkbewegung
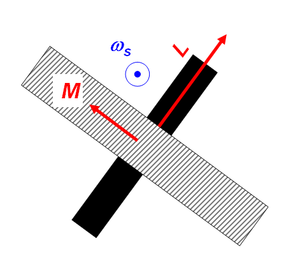
Steht das einwirkende Drehmoment normal zur Winkelgeschwindigkeit, ist die Leistung des Drehmoments gleich Null und der Körper ändert seine Rotationsenergie nicht. So kann jedes schwenkbar gelagerte Rad seinen Drehimpuls bei konstant gehaltener Rotationsenergie ändern. Dazu muss die Achse des rotierenden Rads gedreht werden. Formal gilt ein zur Kreisbewegung analoger Zusammenhang
- [math]\vec M=\vec\omega_S\times\vec L=\frac{d\vec L}{dt}[/math]
Mit ωS ist die Winkelgeschwindigkeit der Schwenkbewegung und nicht etwa die Winkelgeschwindigkeit des sich drehenden Rades gemeint. Die Formel verknüpft drei Grössen, wobei zwei, das Drehmoment und die Winkelgeschwindigkeit der Schwenkbewegung, wahlweise als ursächlich angesehen werden können. Eine Schwierigkeit bei der Anwendung dieser Formel ist die Regel der rechten Hand, die bei allen drei Grössen und beim Vektorprodukt angewendet werden muss
- Drehimpuls: Finger der rechten Hand um das Rad in Rotationsrichtung legen; Daumen zeigt die Richtung des Drehimpulses an
- Winkelgeschwindigkeit der Schwenkbewegung: Finger der rechten Hand in die Ebene legen, in welche die Achse des Rades gekippt wird; Daumen zeigt in Richtung der Winkelgeschwindigkeit der Schwenkbewegung
- Drehmoment: Finger der rechten Hand in Wirkrichtung des Drehmoments legen; Daumen zeigt in Richtung des Drehmoments (Schraube anziehen)
- Vektorprodukt: Daumen parallel zur Winkelgeschwindigkeit der Schwenkbewegung legen; Zeigefinger nach dem Drehimpuls ausrichten; Mittelfinger zeigt in Richtung des Drehmoments.
Trägt man alle drei Vektoren (Drehimpuls, Winkelgeschwindigkeit der Schwenkbewegung, Drehmoment) in eine Skizze ein, ist die Anwendung des Vektorprodukts keine grosse Hexerei.
Beispiel Motorrad: Die Frage eines Yamaha-Fahrers zeigt die Problematik der Kurvenfahrt mit einem Motorrad: "Wenn ich eine Linkskurve einleiten will, drücke ich den Lenker auf der linken Seite nach vorne. Das Vorderrad zeigt also von der Zentrallinie abweichend nach rechts. Dadurch verschiebt sich der Schwerpunkt nach links und das Motorrad fährt eine Linkskurve. Wenn ich jetzt aber besonders langsam fahre (zum Beispiel bei der Fahrübung, wo man eine 8 fahren muss - kennen sicher noch einige von der praktischen Prüfung), dann funktioniert das Ganze umgekehrt. Sprich wenn ich nach links fahren möchte ist der Lenker auch ganz nach links eingeschlagen. Wie funktioniert es also eigentlich, dass das Motorrad eine Kurve fahren kann?"
Wäre die Erklärung mit dem Schwerpunkt richtig, müsst sie auch beim Skibob oder Snowbike funktionieren. Mit diesen Geräten fährt man auch mit hoher Geschwindigkeit in eine Kurve. Der entscheidende Effekt kommt aber vom Drehimpuls des Vorderrades. Drückt man den Lenker links nach vorn, wirkt ein nach unten gerichtetes Drehmoment auf das Vorderrad ein. Weil der Drehimpuls nach links zeigt, kippt das Rad nach links und der Töff neigt sich auf die richtige Seite. Zur Überprüfung dieses Zusammenhangs lege man den Daumen parallel zur Winkelgeschwindigkeit der Schwenkbewegung, also nach hinten. Der Zeigfinger, welcher in Richtung des Drehimpulses anzeigt, weist nach links. Daraus ergibt sich ein nach unten gerichtetes Drehmoment. Und dieses Moment erzeugt der Fahrer, indem er den Lenker mit der linken Hand nach vorne drückt.
Beispiel Wendezeiger: Der Wendezeiger (Turn Indicator) ist ein Kreiselinstrument, das die Winkelgeschwindigkeit des Flugzeuges um die Hochachse anzeigt. Der halbkardanisch gelagerte Kreisel rotiert parallel zur Querachse des Flugzeuges. Nun kann der Käfig, der den Kreisel lagert, um eine parallel zum Flugzeug gerichtete Achse gedreht werden. Diese Drehung ist mit einer Rückstellfeder gekoppelt. Weist der Drehimpulsvektor des Kreisels vom Pilot aus gesehen nach rechts und dreht sich das Flugzeug um die Hochachse nach links, muss ein nach vorne weisendes Drehmoment auf den Kreisel einwirken, damit dieser die Drehbewegung des Flugzeuges mitmacht. Dazu kippt die Kreiselachse leicht nach links, bis die Feder stark genug gespannt ist. Die Stärke der Kippbewegung zeigt so die Grösse der Winkelgeschwindigkeit an.
Beispiel Strahltriebwerk: Fan, Kompressor und Turbine eines Strahltriebwerkes rotieren mit hoher Drehzahl und speichern entsprechend viel Drehimpuls. Fliegt nun ein Flugzeug eine Kurve, muss ein grosses Drehmoment auf das Triebwerk einwirken, damit sich dieses mit dem Flugzeug dreht. Das Drehmoment steht normal zum Triebwerk und liegt in der Kurvenebene drin. Eine schnelle Rotation um die Querachse (unsanfte Landung oder Looping) belastet die Aufhängung der Triebwerke eher noch stärker als der Kurvenflug.
Präzession
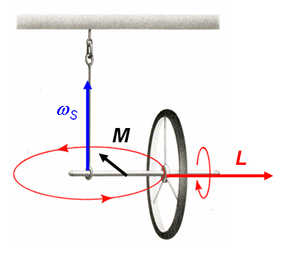
Wirkt auf einen Kreisel über längere Zeit ein Drehmoment ein, das normal zum Drehimpuls gerichtet ist, setzt gemäss der weiter oben aufgeführten Formel eine Schwenkbewegung ein. Die Kreiselachse überstreicht dann den Mantel eines Kegels. Diese Bewegung nennt man Präzession. Im Demonstrationsexperiment zur Präzession (die Skizze zeigt ein etwas anderes Experiment) belastet man einen kardanisch aufgehängten, horizontal rotierenden Kreisel mit einem seitlich angebrachten Zusatzkörper. Die Gewichtskraft dieses Zusatzkörpers erzeugt dann über die Hebelwirkung ein Drehmoment M auf den Kreisel. Weil dieses Drehmoment die Schwenkbewegung mitmacht, stellt sich eine stationäre Präzessionsbewegung ein. Die Präzessionsperiode ist gleich
- [math]T_P=\frac{2\pi}{\omega_S}=\frac{2\pi L}{M}[/math]
Im Demonstrationsversuch hängt man den Zusatzkörper an die anfangs ruhende Achse. Der Kreisel kippt dann zuerst nach unten, um dann in eine Präzessionsbewegung überzugehen, die von einer gedämpften Nutation überlagert wird. Mit der Kippbewegung stellt der Kreisel Drehimpuls für die Präzessionsbewegung zur Verfügung. Würde keine Reibung auftreten, käme der Kreisel nach jeder Nutationsperiode in horizontaler Lage wieder zur Ruhe. Um die Nutation zu verhindern, stösst man beim Aufhängen des Zusatzkörpers den Kreisel so weg, dass er von Anfang an den für die Präzession notwendigen Drehimpuls besitzt. Dann dreht sich der Kreisel anfänglich horizontal. Infolge der Reibung wird er sich dennoch immer stärker vertikal ausrichten.
Beispiel Präzession der Erde: Mond und Sonne wirken mit je einem periodisch anschwellenden Drehmoment auf die Erde ein und versuchen sie aufzurichten. Ursache dieser Einwirkung ist "Äquatorwulst", die rotationsbedingte Abplattung der Erde. Auf diese Einwirkung reagiert die Erde mit einer lunisolaren Präzession. Die Erdachse benötigt für einen einzigen Umlauf auf dem Präzessionskegel zwischen 25.700 und 25.800 Jahre. Dieser Zeitraum wird auch platonisches Jahr genannt. Weil unser Kalender an den Frühlingspunkt (Äquinoktium) gebunden ist, verschieben sich die Monate infolge der Präzession etwa alle 2000 Jahre um ein Sternzeichen.
Unwucht
Rotierende Maschinenelemente wie Räder, Propeller oder Turbinen müssen ausgewuchtet sein, damit die Lager nicht unnötig belastet werden. Man unterscheidet zwischen statischer und dynamischer Unwucht. Bei der statischen Unwucht ändert sich der Impuls und bei der dynamischen der Drehimpuls bei konstant gehaltener Bewegungsenergie. Zur Erklärung dieses Phänomens gehen wir von einer ausgewuchteten Scheibe aus, die entlang des Umfangs mehrere, achsenparallele Gewindelöcher aufweist. In diese Bohrungen können kurze Schrauben eingedreht werden, um so gezielt eine Unwucht zu erzeugen.
statische Unwucht
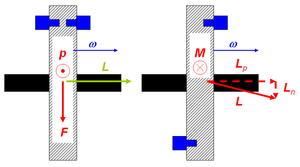
Dreht man zwei kurze Schrauben (Masse mS) von beiden Seiten in das gleiche Gewindeloch, verschiebt sich der Massenmittelpunkt des Gesamtsystems weg von der Scheibenachse. Der Impulsinhalt von rotierender Scheibe und Schrauben ist gleich gross wie der eines punktförmigen Körpers gleicher Masse, der sich im Abstand rMMP auf einer Kreisbahn um die Achse bewegt
- [math]p=2m_Sv_S=2m_Sr_S\omega=mr_{MMP}\omega[/math]
Damit sich der Impulsinhalt synchron mit der Drehung ändert, muss von den Lagern eine Kraft einwirken
- [math]F_L=\omega p=mr_{MMP}\omega^2[/math]
Die Lagerkraft steigt quadratisch mit der Drehzahl. Deshalb müssen schnell drehende Körper speziell gut ausgewuchtet sein.
dynamische Unwucht

Befestigt man die Schrauben so in zwei gegenüber liegenden Löchern, dass ihre Köpfe auf je einer Seite der Scheibe heraus ragen, entsteht eine dynamische Unwucht. Obwohl der Massenmittelpunkt des Gesamtsystems weiterhin auf der Drehachse liegt, werden die Lager mit zunehmender Drehzahl belastet. Zur Analyse bilden wir den Bahndrehimpuls der beiden Schrauben. Dieser Bahndrehimpuls steht leicht schief zur Scheibenachse und bewegt sich auf einem Kreiskegel. Nun bleibt die zur Drehachse (Winkelgeschwindigkeit) parallele Komponente des Drehimpulses erhalten. Die Radialkomponente wird dagegen durch die Drehbewegung herum gewirbelt, macht also eine andauernde Schwenkbewegung. Das zugehörige Drehmoment, das von den Lagern aufgebracht werden muss, ist gleich
- [math]M_L=\omega L_n=2m_S r_S z_S\omega^2[/math]
wobei zS den Abstand der Massenmittelpunkte der Schrauben von der Symmetrieebene der Scheibe misst. Nun kann man jedem drehbar gelagerten Körper bezüglich der gegebenen Achse ein Deviations- oder Zentrifugalmoment JD zuschreiben, das den Zusammenhang zwischen Radialkomponente des Drehimpulses und Winkelgeschwindigkeit beschreibt
- [math]L_n=J_D\omega[/math]
Das Drehmoment, das von den Lagern auf den Körper einwirken muss, um dessen Drehachse zu stabilisieren, ist dann gleich
- [math]M_L=J_D\omega^2[/math]
Hält man die Achse eines rotierenden Körpers mit Hilfe von zwei Lagern stabil und misst je eine Komponente der Lagerkräfte, erhält man zwei zeitabhängige Signale. Aus diesen Lagerkräften können die resultierende Kraft und das resultierende Drehmoment berechnet werden. Beide Grössen nehmen quadratisch mit der Drehzahl zu. Die resultierende Kraft ist zudem proportional zum Abstand des Schwerpunkts von der Drehachse und das Drehmoment nimmt linear mit dem Deviationsmoment zu.
Kontrollfragen
- Formulieren Sie die Impuls- und die Drehimpulsbilanz bezüglich eines starren Körpers mit Ihren eigenen Worten.
- Worin unterscheidet sich die Drehmechanik von der Translationsmechanik?
- Formulieren Sie die Energiebilanz bezüglich eines starren Körpers mit Ihren eigenen Worten.
- Wie muss man einen Ziegelstein hochwerfen, damit er stabil rotiert?
- Sie halten die beiden Enden der Achse eines rotierenden Rades mit den Händen fest. Überlegen Sie sich, was passiert, wenn man das eine Ende der Achse gegen sich zieht? die Achse einseitig nach oben drückt? Die Antwort können Sie im Versuch herausfinden, aber achten Sie auf Ihre Finger.
- Wieso verschieben sich die Sternzeichen gegen den Kalender?
- Wie unterscheiden sich dynamische und statische Unwucht?
- Wie verändert sich bei einer Unwucht die Belastung der Lager mit steigender Drehzahl?
Antworten zu den Kontrollfragen
- Die Summe über alle Kräfte (Oberflächenkräfte und Gewichtskraft) verursacht die Änderungsrate des Impulsinhalts. Die Summe über alle Drehmomente (reine und einer Kraft zugeordnete) verursacht die Änderungsrate des Drehimpulsinhalts.
- In der Drehmechanik ist die Trägheit kein Skalar wie die Masse sondern ein Tensor. Die Drehbewegungen bilden nur eine Gruppe und keinen Vektorraum wie die Verschiebungen.
- Die Summe über die Leistungen aller Kräfte (Oberflächenkräfte und Gewichtskraft) plus die Summe über die Leistungen aller reinen Drehmomente (ohne die einer Kraft zugeordneten Drehmomente) sind gleich der Änderungsrate der kinetischen und der Rotationsenergie.
- Der Ziegelstein muss so geworfen werden, dass er um eine Achse parallel zu kürzesten Kante (grösstes Massenträgheitsmoment) oder zur längsten Kante (kleinstes Massenträgheitsmoment) rotiert.
- Ohne Skizze werden Sie kaum auf die richtige Lösung kommen: zeichnen Sie den Vektor des Drehimpulses ein, markieren Sie die Einwirkung, das Drehmoment, mit einem weiteren Pfeil; die Winkelgeschwindigkeit der Schwenkbewegung muss dann die oben formulierte Gesetzmässigkeit erfüllen.
- Sonne und Mond versuchen die Achse der Erde aufzurichten. Diese reagiert mit einer Präzessionsbewegung. Weil sich der Kalender am Frühlingspunkt (Schnittpunkt der Ekliptik mit dem Äquator) orientiert, wandern die Monate über die Sternzeichen.
- Bei der statischen Unwucht liegt der Massenmittelpunkt nicht auf der Drehachse. Deshalb ändert sich der Impulsinhalt periodisch, wodurch die Lager mit einer umlaufenden Kraft belastet werden. Bei der dynamischen Unwucht liegt die Drehachse nicht auf einer Hauptachse des Körpers. Deshalb ändert sich der Drehimpulsinhalt periodisch, wodurch die Lager mit einem umlaufenden Drehmoment belastet werden.
- Lagerkraft und Lagerdrehmoment nehmen quadratisch mit der Drehzahl zu.
Links
- Videoaufzeichnung
- Unwucht auf Youtube
- Schwenkbewegung auf Youtube
- Kurzfassung auf Youtube