Widerstand und Speicher

Schema der Hydraulik beim A340

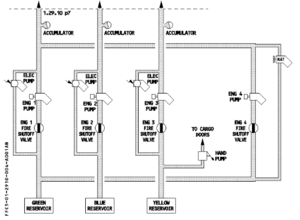
Der Airbus A340 besitzt drei unabhängige Hydraulikkreise (Betriebsdruck 3000 psi oder 207 bar), die mit blau (blue), grün (green) und gelb (yellow) bezeichnet werden. Das nebenstehend abgebildete Schema zeigt, wie die drei Hydrauliksysteme mit Energie beladen werden. Das grüne System wird von zwei Triebwerken, einer elektrischen Pumpe und einer Windturbine, Ram Air Turbine (RAT) genannt, mit Energie versorgt. Ein weiteres Triebwerk und bei Ausfall desselben eine elektrische Pumpe beladen das blaue System mit Energie. Das gelbe System bekommt seine Energie vom vierten Triebwerk und einer elektrischen Pumpe. Im Normalfall beladen nur die Triebwerke die hydraulische Systeme mit Energie. Mit der Handpumpe des gelben Systems kann notfalls die Gepäckraumtür geöffnet werden. Jede Operation, wie z.B. das Fahrwerk ausfahren, lässt sich von zwei hydraulischen Systemen ausführen. Diese Redundanz dient der Sicherheit.

Ein Teil der Energie wird in den Leitungen dissipiert. Zudem besitzt jedes System mindestens einen Hydraulikspeicher (Accumulator), der kurzfristig Energie liefern kann und die Druckspitzen glättet. Mit je einer Eigenschaft der Leitungen und der Speicher, dem Widerstand bzw. der Kapazität, wollen wir uns in dieser Vorlesugn beschäftigen.

Lernziele

In dieser Vorlesung werden Sie lernen

• worin der Unterschied zwischen laminarer unnd turbulenter Strömungen besteht
• wie bei laminarer und bei turbulenter Strömung die Druckdifferenz mit dem Volumenstrom zusammenhängt
• wie man parallel und seriell geschaltete Widerstände rechnerisch zusammenfasst
• wie die dissipierte Leistung berechnet wird
• wie die Kapazität eines Speichers definiert ist
• wie man die hydraulisch gespeicherte Energie berechnet

Widerstand

Jeder Leitungsabschnitt, jedes Ventil und alle Verzweigungen (Knoten) wirken dem Ölstrom entgegen. Der Druck fällt in all den Leitungen und Armaturen ab, sobald Öl hindurch fliesst. Das Verhältnis aus Druckabfall zu Volumenstrom nennt man Widerstand.

laminar und turbulent

Rohrströmung

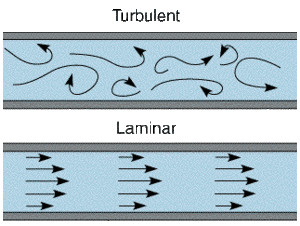
Eine Flüssigkeit, die langsam durch ein Rohr strömt, bewegt sich in der Rohrmitte am schnellsten. An der Rohrwand bleibt die Flüssigkeit haften (Benetzung). Dazwischen schieben sich die einzelnen Schichten wie die Häute einer zylinderförmigen Zwiebel übereinander. Dieses Strömungsverhalten nennt man laminar. Einfach strukturierte Flüssigkeiten, sogenannte Newtonsche Fluide, bilden bei laminarer Strömung ein parabelförmiges Geschwindigkeitsprofil. Erhöht man den Durchsatz, beginnen sich einzelne Wirbel zu bilden. Mit zunehmendem Volumenstrom treten immer mehr Wirbel auf, bis sich die Strömung völlig chaotisch verhält.

linear und quadratisch

In einer laminar strömenden Flüssigkeit, nimmt die die Druckdifferenz über einem bestimmten Rohrstück proportional mit der Stärke des Volumenstroms zu. Diesen Proportionalitätsfaktor nennen wir Strömungswiderstand und bezeichnen ihn mit R_V

[math]\Delta p = R_V I_V[/math]

Bei einer turbulenten Strömung steigt die Druckdifferenz quadratisch mit der Volumenstromstärke. Bezeichnen wir den Proportionalitätsfaktor mit k, kann das turbulente Widerstandsverhalten wie folgt beschrieben werden

[math]\Delta p = k I_V^2[/math]

Der Strömungswiderstand R_V hat die Einheiten Pas/m³, der turbulente Faktor k wird in Pas²/m⁶ gemessen.

laminares und quadratisches Gesetz

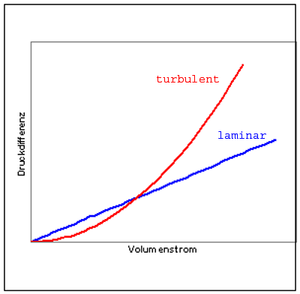
In erster Näherung darf man nun behaupten, dass die Strömung in einem Rohr so lange laminar bleibt, bis der turbulente Druckabfall über einem Rohr grösser wird als der laminare. Sobald dies eintritt, schlägt die Strömung von laminar auf turbulent um. Diese Bedingung liefert einen Wert für den kritischen Strom

[math]I_{V_{krit}} = \frac {R_V}{k}[/math]

bzw. den kritischen Druck

[math]\Delta p_{krit} = \frac {R_V^2}{k}[/math]

Der Umschlag von laminar auf turbulent erfolgt aber nicht genau bei einer ganz bestimmten Volumenstromstärke. Die Strömung wird vielmehr in einem gewissen Strömungsbereich immer chaotischer. Je dichter die Flüssigkeit und je weiter das Rohr ist, desto früher schlägt die Stromung um. Die Viskosität der Flüssigkeit verzögert den Übergang von laminar zu turbulent.

Sowohl der Widerstand als auch der Faktor k der turbulenten Strömung können bei einem langen Rohr mit Hilfe einer Formel berechnet werden. Für kompliziertere Leitungsabschnitte existieren weitere Berechnungsformeln oder Erfahrungswerte. Heute lassen sich diese Grössen für die unterschiedlichsten Geometrien mit Hilfe eines Rechenprogrammes (Computational Fluid Dynamics) ermitteln.

Serieschaltung

Fliesst der gleiche Ölstrom nacheinander durch verschiedene Leitungsabschnitte oder Armaturen, fällt der Druck über jedem Element ab. Fasst man die so in Serie geschalteten Elemente zu einem einzigen System zusammen, ist die gesamte Druckdifferenz gleich der Summe der einzelnen Druckänderungen. Folglich darf man dem Gesamtsystem einen Widerstand zuschreiben, der gleich der Summe der Einzelwiderstände ist

[math]R_{V_{tot}} = \sum_i R_{V_i}[/math]

Diese Überlegung gilt auch bei turbulenter Strömung

[math]k_{tot} = \sum_i k_i[/math]

Parallelschaltung

Parallel geschaltete Leitungen lassen mehr Öl durch als eine einzige. Entsprechend kleiner ist der Gesamtwiderstand. Fasst man mehrere Leitungsabschnitte, die sowohl am Eingang als auch am Ausgang miteinander verbunden sind, zu einem Gesamtsystem zusammen, ist der durchfliessende Volumenstrom gleich der Summe aller Einzelströme. Die Druckdifferenz, die über allen Abschnitten gleich gross ist, überträgt sich auf das Gesamtsystem. Nun gilt

[math]\frac {I_V}{\Delta p} = \frac {1}{R_V} = \frac {\sum_i I_{V_i}}{\Delta p} = \sum_i \left(\frac {1}{R_{V_i}}\right)[/math]

Der Reziprokwert des Strömungswiderstandes eines Gesamtsystems ist bei Parallelschaltung gleich der Summe über alle Reziprokwerte der Einzelwerte. Der Gesamtwiderstand ist damit kleiner als der kleinste Einzelwiderstand.

Bei turbulenter Strömung kann eine ähnliche Überlegung angestellt werden: der Gesamtvolumenstrom ist gleich der Summe aller Einzelströme und der Druckabfall bleibt beim Gesamtsystem gleich wie bei jedem Element. Nur gilt das quadratische Widerstandsgesetz. Folglich erhält man eine ander Additionsvorschrift

[math]\frac {1}{k^2} = \sum_i \left(\frac {1}{k_i^2}\right)[/math]

dissipierte Leistung

Strömt eine Flüssigkeit in einem Rohr nach oben oder muss sie bei einer Verengung schneller fliessen, wird der Druck kleiner, weil die Energie auf das Gravitationsfeld oder die Bewegung übertragen wird. Der Ölstrom setzt immer dann Prozessleistung frei, wenn der Druck über einer bestimmten Strecke abfällt. Vermindert sich der Druck infolge Reibung, wird die Energie dissipiert. Bei der Dissipation sagt man oft, dass die Energie verloren geht oder sogar vernichtet wird. Nun kann Energie weder verloren gehen noch vernichtet werden. Die Energie wird vielmehr auf den Träger Entropie umgeladen. Diese Entropie wird direkt im Reibungsvorgang erzeugt. In der Umgangssprache sagen wir dann oft, dass durch Reibung Wärme entsteht.

Die Prozessleistung ist - wie Sie in der letzten Vorlesung gehört haben - gleich Druckdifferenz mal Volumenstromstärke. Setzt man das lineare Widerstandsgesetz ein, erhält man

[math]P_{diss} = \Delta p I_V = R_V I_V^2[/math]

Bei turbulentem Strömungsverhalten wächst die dissipierte Leistung sogar mit der dritten Potenz der Volumenstromstärke

[math]P_{diss} = \Delta p I_V = k I_V^3[/math]

In hydraulischen Systemen strömt das Öl in der Regel laminar. Verdoppelt man nun bei einer hydraulischen Leitung den Durchsatz, vervierfacht sich die dissipierte Prozessleistung bei doppeltem Druckabfall. Bei Wasserleitungen kann man davon ausgehen, dass die Strömung turbulent ist. Diese Turbulenzen hört man im ganzen Haus, wenn jemand morgens um vier Uhr duscht. Verdoppelt man bei einer Wasserleitung den Dutchsatz, verachtfacht sich die Prozessleistung. Der Druckabfall beträgt dann das Vierfache. Das weiss auch die Feuerwehr. Weil der Motor einer Pumpe nur eine beschränkte Leistung abzugeben vermag, kann eine einzige Transportleitung nur eine ganz bestimmte Wassermenge zum Brandherd befördern.

Speicher

Reine Leitungsnetze, die nur Energie übertragen, aber nicht speichern können, sind oft instabil. Um die Stabilität zu erhöhen, werden zusätzliche Speicher angebracht. In hydraulischen Systemen setzt man Feder- und Blasenspeicher ein.

Speicher findet man in allen Zweigen der Physik. Die Tabelle gibt einen Überblick über häufig verwendete Speicher

Gebiet	Objekt	Menge	Potenzial
Hydrodynamik	Blasenspeicher	Volumen	Druck
Elektrodynamik	Kondensator	Ladung	Spannung
Translationsmechanik	Hammer	Impuls	Geschwindigkeit
Rotationsmechanik	Schwungrad	Drehimpuls	Winkelgeschwindigkeit
Thermodynamik	Wärmespeicher	Entropie	Temperatur

In der Umgangssprache nennt man den Impuls oft Schwung oder Wucht, den Drehimpuls Drall und die Entropie Wärme.

Kapazität

Der Begriff Kapazität (lat.: capacitas = „Fassungsvermögen“) bezeichnet ganz unterschiedliche Eigenschaften wie die Speicherfähigkeit eines Mediums (Speicherkapazität), den maximaler Durchsatz bei einer Datenleitung (Kanalkapazität) bzw. einer Strasse, oder einfach das Fassungsvermögen eines Gefässes. In der Physik versteht man unter der Kapazität eine Speicherfähigkeit pro Potenzialänderung. Die hydraulische Kapazität ist deshalb gleich der Volumenänderung eines Speichers dividiert durch die damit verbundene Druckänderung

[math]C_V = \frac {\Delta V}{\Delta p}[/math]

Eine grosse Kapazität bedeutet demnach, dass ein Speicher viel Flüssigkeit aufnehmen kann, ohne dass der Druck stark ansteigt. Die Einheit der hydraulischen Kapazität ist m³/Pa. Weil der Kubikmeter eine grosse und das Pascal eine sehr kleine Einheit ist, sind die Zahlenwerte für die Kapazität oft sehr klein.

konstante Kapazität

Zylinderförmige Gefässe und federbelastete Speicher weisen eine Kapazität auf, die nicht vom Füllstand abhängt. In der Systemdynamik zählt man diese Speicher zu den linearen Elementen. Ist die Kapazität bekann, kann aus der Druckänderung die Volumenzunahme berechnet werden

[math]\Delta V = C_V \Delta p[/math]

nichtlineare Speicher

Blasenspeicher sind nichtlinear. Im Praktikum werden wir Petflaschen als Blasenspeicher einsetzen. Wird eine Petflasche nicht zu schnell mit Wasser gefüllt, gehorcht die eingeschlossene Luftblase dem Gesetz von Boyle-Mariotte, wonach das Produkt aus Absolutdruck und Volumen der Luftblase konstant bleibt; Druck und Volumen verhalten sich umgekehrt proportional zueinander. Überträgt man dieses Verhalten auf das Wasser, erhält man das folgende Speicherverhalten

[math]p = p_0 \frac {V_0}{V_0 - V}[/math]

V steht für das in der Petflasche gespeicherte Wasservolumen, p₀ entspricht dem Luftdruck und mit V₀ ist das gesamte Fassungsvermögen der Petflasche gemeint (eine 1.5 Liter hat die Petflasche ein Fassungsvermögen von mehr als anderthalb Liter).

gespeicherte Energie

Ein hydraulischer Speicher nimmt neben dem Volumen mindestens noch die Energie auf, die zusammen mit dem Volumenstrom hinein transportiert wird. Will man nun wissen, wie viel Energie der Speicher hydraulisch abgeben kann, muss man ermitteln, wie viel Energie vorher hinein transportiert worden ist. Also summiert (integriert) man bei anfänglich leerem Speicher den zugeordneten Energiestrom über die Zeit auf.

konstante Kapazität

Schickt man in einen leeren Speicher einen konstanten Volumenstrom, steigt der Druck linear in der Zeit an. Stellt man diesen Prozess für einen Speicher mit konstanter Kapazität und Anfangsdruck Null im Volumenstrom-Druck-Zeit-Schaubild dar, erhält man ein Prisma mit dreieckiger Grundfläche. Das Volumen dieses Körpers beschreibt dann der geflossenen bzw. gespeicherten Energie. Die eine Seitenfläche des Prismas entspricht dem geflossenen bzw. gespeicherten Volumen. Nimmt man diese Seite als Grundfläche, ist die Energie gleich dem Volumen eines Keils mit dem Enddruck als Höhe. Das Volumen eines Keisl mit der Grundfläche V und der Höhe p ist gleich

[math]W=\frac{1}{2}pV=\frac{1}{2}C_Vp^2=\frac{1}{2C_V}V^2[/math]

Der erste Ausdruck für die Energie in dieser Formel kann direkt interpretiert werden: das Volumen ist im Mittel bei halbem Druck in den Speicher transportiert worden. Beim zweiten Term ist das Volumen und beim dritten der Druck mit Hilfe des kapazitiven Gesetzes eliminiert worden.

Ein federbelasteter Hydraulikspeicher verhält sich liniear, ist aber in der Regel vorgespannt. Der Druck beginnt dann nicht bei Null sondern steigt von einem bestimmten Wert p₀ an hoch. Im Volumenstrom-Druck-Zeit-Schaubild erscheint die Energie bei konstantem Volumenstrom als abgeschnittener Keil

[math]W=p_{mittel}V=\frac{p+p_0}{2}V=\frac{p+p_0}{2}C_V(p-p_0)=\frac{C_V}{2}(p^2-p_0^2)[/math]

Diese Formel ist mit der ersten vergleichbar: Ist bei einem Speicher mit konstanter Kapazität der Anfangsdruck grösser als Null, muss die Energie, die man von Null her hätte einbringen müssen, um diesen Anfangsdruck zu erzeugen, abgezogen werden.

beliebiges Speicherverhalten

Ein Blasenspeicher oder eben eine Petflasche verhält sich nichtlinear. Drückt man immer mehr Wasser in eine Petflasche hinein, wird die Luftblase wohl immer kleiner, aber im Sinne eines umgekehrten Dreisatzes und folglich nicht linear mit dem Druck. Um im diesem Fall die gespeicherte Energie zu rechnen, gehen wir von der dynamischen zur statischen Betrachtungsweise über. In einem sehr kurzen Zeitintervall Δt transportiert der Volumenstrom die folgende Energiemenge

[math]\Delta W=I_W\Delta t=p I_V\Delta t = p\Delta V[/math]

Nun werden von einem hydaulischen Speicher sowohl Volumen als auch Energie gemeinsam aufgenommen. Also gilt der Zusammenhang zwischen transportiertem Volumen und Energie auch für den Zuwachs im Speicher

[math]\Delta W=p\Delta V[/math]

Diese Formel muss in kleinen Schritten ausgewertet werden, weil der Druck mit dem Volumen stetig ansteigt. Zeichnet man nun das Verhalten eines Speichers in ein Druck-Volumen-Diagramm ein, erhält man eine Linie, die Speichercharakteristik genannt wird. In diesem Diagramm entspricht die Energiezunahme (Druck mal Volumenzunahme) der Fläche eines kleinen Rechtecks. Denkt man sich den Ladevorgang als Summe über mehrere kleine Volumenaufnahmen, erscheint die Energie als Fläche unter der zugehörigen "Treppe":

Die von einem Speicher aufgenommene Energie entspricht der Fläche unter dem p-V-Diagramm

Zylinderförmige Gefässe und federbelastete Speicher haben eine lineare Charakteristik. Im p-V-Diagramm nimmt die von diesen Elementen aufgenommene Energie die Form eines Dreiecks bzw. eines Trapezes an. Wertet man das Dreieck aus, erhält man die erste der in diesem Abschnitt aufgeführten Formel. Die zweite Formel ergibt sich aus dem Trapez.